题目内容
4. 如图,在△ABC中,CD平分∠ACB,DE∥BC交AC于E,若DE=7,AE=5,AC的长为12.
如图,在△ABC中,CD平分∠ACB,DE∥BC交AC于E,若DE=7,AE=5,AC的长为12.
分析 由CD平分∠ACB,可得∠ACD=∠BCD,又DE∥BC,所以,∠EDC=∠BCD,即∠ECD=∠EDC,所以,△ECD是等腰三角形,CE=DE,又AE=5,DE=7,即可求得.
解答 解:∵由CD平分∠ACB,
∴∠ACD=∠BCD,
又∵DE∥BC,
∴∠EDC=∠BCD,即∠ECD=∠EDC,
∴△ECD是等腰三角形,
∴CE=DE,
又∵AE=5,DE=7,
∴AC=AE+EC=5+7=12;
故答案为:12
点评 本题主要考查了等腰三角形的判定与性质和平行线的性质,知道两边相等的三角形是等腰三角形,两直线平行,内错角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.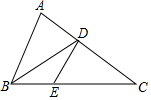 如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )
如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )
 如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )
如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )| A. | 4 | B. | 6 | C. | $\frac{5}{3}$ | D. | $\frac{10}{3}$ |
14.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
则下列判断正确的是( )
| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -3 | 1 | 3 | 1 | … |
| A. | 抛物线开口向上 | B. | 抛物线与y轴交于负半轴 | ||
| C. | 当x=4时,y>0 | D. | 方程ax2+bx+c=0的正根在3与4之间 |
 如图,竖立在点B处的标杆AB高2.5m,站立在点F处的观察者从点E处看到标杆顶A、树顶C在一条直线上.测得BD=9m,FB=3m,EF=1.7m,求树高CD.
如图,竖立在点B处的标杆AB高2.5m,站立在点F处的观察者从点E处看到标杆顶A、树顶C在一条直线上.测得BD=9m,FB=3m,EF=1.7m,求树高CD.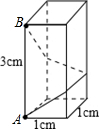 如图,长方体的底面是边长为1cm 的正方形,高为3cm.
如图,长方体的底面是边长为1cm 的正方形,高为3cm. 如图,亮亮书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么亮亮画图的依据是两角和它们的夹边分别相等的两个三角形全等.
如图,亮亮书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么亮亮画图的依据是两角和它们的夹边分别相等的两个三角形全等.