题目内容
14. 如图,已知在△ABC中,△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.求证:MN=CN-BM.
如图,已知在△ABC中,△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.求证:MN=CN-BM.
分析 只要证明BM=OM,ON=CN,即可解决问题.
解答 证明:∵ON∥BC,
∴∠NOB=∠OBD
∵BO平分∠ABD,
∴∠ABO=∠DBO,
∴∠MOB=∠OBM,
∴BM=OM
∵ON∥BC,
∴∠NOC=∠OCD
∵CO平分∠ACB,
∴∠NCO=∠BCO,
∴∠NCO=∠NOC,
∴ON=CN
∵ON=OM+MN,ON=CN,OM=BM,
∴CN=BM+MN,
∴MN=CN-BM.
点评 此题考查等腰三角形的判定和性质、平行线的性质等知识,解题的关键是证明等腰三角形,属于基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
9.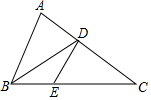 如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )
如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )
 如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )
如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )| A. | 4 | B. | 6 | C. | $\frac{5}{3}$ | D. | $\frac{10}{3}$ |
3. 小聪用直尺和圆规作角平分线,方法如下:①利用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON;②分别过M、N作OM、ON的垂线,交于点P;③作射线OP,则OP为∠AOB的平分线,小聪用尺规作角平分线时,用到的三角形全等的判定方法是( )
小聪用直尺和圆规作角平分线,方法如下:①利用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON;②分别过M、N作OM、ON的垂线,交于点P;③作射线OP,则OP为∠AOB的平分线,小聪用尺规作角平分线时,用到的三角形全等的判定方法是( )
 小聪用直尺和圆规作角平分线,方法如下:①利用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON;②分别过M、N作OM、ON的垂线,交于点P;③作射线OP,则OP为∠AOB的平分线,小聪用尺规作角平分线时,用到的三角形全等的判定方法是( )
小聪用直尺和圆规作角平分线,方法如下:①利用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON;②分别过M、N作OM、ON的垂线,交于点P;③作射线OP,则OP为∠AOB的平分线,小聪用尺规作角平分线时,用到的三角形全等的判定方法是( )| A. | SSS | B. | SAS | C. | ASA | D. | HL |
4.某校九年级数学模拟测试中,六名学生的数学成绩如下(单位:分):110,106,109,111,108,110,下列关于这组数据描述正确的是( )
| A. | 众数是110 | B. | 方差是16 | C. | 平均数是109.5 | D. | 极差是6 |
 如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=140°,则∠AOC=55°;∠BOC=35°.
如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=140°,则∠AOC=55°;∠BOC=35°. 如图,一位同学做了一个斜面装置进行科学实验,△ABC是该装置左视图,∠ACB=90°,∠B=15°,为了加固斜面,在斜面AB的中点D处连结一条支撑杆CD,量得CD=6.
如图,一位同学做了一个斜面装置进行科学实验,△ABC是该装置左视图,∠ACB=90°,∠B=15°,为了加固斜面,在斜面AB的中点D处连结一条支撑杆CD,量得CD=6.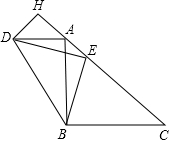 如图,在△ABC中,BA=BC,∠ABC=90°,AD∥BC,点E在边AC上,且∠DEB=90°,DH⊥AC于H.
如图,在△ABC中,BA=BC,∠ABC=90°,AD∥BC,点E在边AC上,且∠DEB=90°,DH⊥AC于H.