题目内容
1.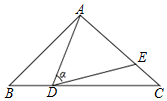 如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,下列结论:
如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,下列结论:①△ADE∽△ACD;
②当BD=6时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD为8或$\frac{25}{2}$;
其中正确的结论是①②③.(把你认为正确结论的序号都填上)
分析 ①根据有两组对应角相等的三角形相似即可证明;
②由BD=6,则DC=10,证得对应边不相等,△ABD与△DCE不全等;
③由△DCE为直角三角形,可得有两种可能:①∠CED=90°②∠EDC=90°,然后分别去分析,利用等腰三角形的性质与相似三角形的性质,求得答案.
解答 解:①∵AB=AC,
∴∠B=∠C,
又∵∠ADE=∠B
∴∠ADE=∠C,
∴△ADE∽△ACD;
故①正确,
②∵BD=6,BC=16,
∴CD=10,
∵AB=AC,
∴∠B=∠C,
∵∠ADB=180°-α-∠CDE,∠CED=180°-α-∠CDE,
∴∠ADB=∠DEC,
在△ABD与△CDE中,$\left\{\begin{array}{l}{∠B=∠C}\\{∠ADB=∠DEC}\\{AB=CD}\end{array}\right.$,
∴△ABD≌△CDE,
故②正确;
③△DCE为直角三角形,有以下两种可能:①∠CED=90°②∠EDC=90°.
①当∠CED=90°时,即∠AED=90°,由①可知:△ADE∽△ACD,
∴∠ADC=∠AED,
∵∠AED=90°,
∴∠ADC=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
∴BD=8.  ②当∠EDC=90°时,
②当∠EDC=90°时,
∵∠ADE+∠EDC=∠B+∠BAD,∠ADE=∠B,
∴∠BAD=∠EDC=90°,
如图,过A作AF⊥BC于F,则BF=8,
∵∠B是公共角,∠AFB=∠BAD=90°,
∴△BFA∽△BAD,
∴$\frac{AB}{BD}$=$\frac{BF}{AB}$,
∴BD=$\frac{25}{2}$.
综上所述,△DCE为直角三角形时,BD=8或BD=$\frac{25}{2}$.
故③正确.
故答案为:①②③.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

| A. | 5 | B. | 5或-5 | C. | -5 | D. | -5或1 |
 某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出):根据以上信息解答下列问题:
某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出):根据以上信息解答下列问题:学生孝敬父母情况统计表:
| 选项 | 频数 | 频率 |
| A | m | 0.15 |
| B | 60 | p |
| C | n | 0.4 |
| D | 48 | 0.2 |
(2)求表中m,n,p的值,并补全条形统计图.
(3)该校有1600名学生,估计该校全体学生中选择B选项的有多少人?
 如图,在平面直角坐标系中.直线y=-x+3与x轴交于点B,与y轴交于点C,抛物线y=ax2+bx+c经过B,C两点,与x轴负半轴交于点A,连结AC,tan∠CAB=3
如图,在平面直角坐标系中.直线y=-x+3与x轴交于点B,与y轴交于点C,抛物线y=ax2+bx+c经过B,C两点,与x轴负半轴交于点A,连结AC,tan∠CAB=3 如图,在△ABC中,BE、CD相交于点E,∠A=76°,∠ACD=37°,∠2=143°.求:∠1和∠DBE的度数.
如图,在△ABC中,BE、CD相交于点E,∠A=76°,∠ACD=37°,∠2=143°.求:∠1和∠DBE的度数.