Question

4．如图，在△ABC和△DEF中，AC=DF，BC=EF，∠ABC=∠DEF，且∠ABC，∠DEF都是钝角，求证：△ABC≌DEF．

Answer 1

分析 过点C作CM⊥AB，过点F作FN⊥DE，利用全等三角形的判定和性质证明CM=FN，再利用直角三角形的判定证明即可．

解答 证明：过点C作CM⊥AB，过点F作FN⊥DE，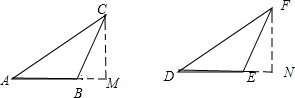

在Rt△CBM与Rt△FEN中
$\left\{\begin{array}{l}{∠CMB=∠FNE=90°}\\{∠CBM=∠FEN}\\{BC=EF}\end{array}\right.$，
∴Rt△CBM≌Rt△FEN（AAS），
∴CM=FN，
在Rt△ACM与Rt△DFN中
$\left\{\begin{array}{l}{AC=DF}\\{CM=FN}\end{array}\right.$，
∴Rt△ABM≌Rt△FEN（HL），
∴∠A=∠D，
在△ABC与△DEF中
$\left\{\begin{array}{l}{∠ABC=∠DEF}\\{∠A=∠D}\\{AC=DF}\end{array}\right.$，
∴△ABC≌DEF（AAS）．

点评 此题考查全等三角形的判定，关键是过点C作CM⊥AB，过点F作FN⊥DE．