题目内容
19.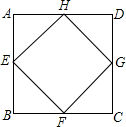 如图,点E,F,G,H分别是正方形ABCD四条边上的中点,求证:四边形EFGH是正方形.
如图,点E,F,G,H分别是正方形ABCD四条边上的中点,求证:四边形EFGH是正方形.
分析 先由三角形的中位线定理求出四边相等,然后由AC⊥BD入手,进行正方形的判断.
解答 证明:连接AC、BD,
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
在△ABC中,F、G分别是AB、BC的中点,
故可得:FG=$\frac{1}{2}$AC,同理EH=$\frac{1}{2}$AC,GH=$\frac{1}{2}$BD,EF=$\frac{1}{2}$BD,
在四边形ABCD中,AC=BD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
在△ABD中,E、H分别是AB、AD的中点,
则EH∥BD,
同理GH∥AC,
又∵AC⊥BD,
∴EH⊥HG,
∴四边形EFGH是正方形.
点评 此题考查了正方形的判定,解题的关键是掌握三角形中位线定理、理解既是矩形又是菱形的四边形是正方形.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
10.小明从家出发,先向东走350m到小亮家,然后它们又向南走500m到老师家,如果以老师家的位置为平面直角坐标系的坐标原点,正东方向为x轴正方向为x轴正方向,正北方向为y轴正方向,那么小明家的位置可记为( )
| A. | (350,500) | B. | (-350,-500) | C. | (350,-500) | D. | (-350,500) |
7.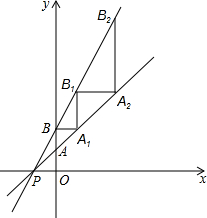 如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )
如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )
 如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )
如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )| A. | (63,64) | B. | (65,64) | C. | (31,32) | D. | (127,128) |
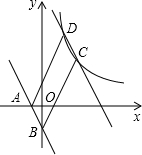 如图,直线AB:y=kx+b(k≠0)过点A(-1,0)和B(0,-2),
如图,直线AB:y=kx+b(k≠0)过点A(-1,0)和B(0,-2),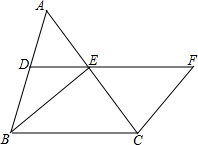 如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到F,使EF=BE,连接CF.
如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到F,使EF=BE,连接CF.