题目内容
对于正数n,规定f(n)=
,例如f(3)=
=
,f(
)=
=
.
(1)求f(2)和f(
)的值;
(2)计算:f(
)+f(
)+…+f(
)+f(1)+f(2)+f(3)+…+f(2013)+f(2014)
| n |
| 1+n |
| 3 |
| 1+3 |
| 3 |
| 4 |
| 1 |
| 3 |
| ||
1+
|
| 1 |
| 4 |
(1)求f(2)和f(
| 1 |
| 2 |
(2)计算:f(
| 1 |
| 2014 |
| 1 |
| 2013 |
| 1 |
| 2 |
考点:有理数的混合运算
专题:新定义
分析:(1)把n=2与n=
代入计算即可求出f(2)和f(
)的值;
(2)归纳总结得到f(n)+f(
)=1,原式结合后相加即可得到结果.
| 1 |
| 2 |
| 1 |
| 2 |
(2)归纳总结得到f(n)+f(
| 1 |
| n |
解答:解:(1)f(2)=
=
,f(
)=
=
;
(2)根据题意得:f(n)+f(
)=
+
=
=1,
则原式=[f(
)+f(2014)]+[f(
)+f(2013)]+…+[f(
)+f(2)]+f(1)=1+1+…+1+
=2013
.
| 2 |
| 1+2 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
1+
|
| 1 |
| 3 |
(2)根据题意得:f(n)+f(
| 1 |
| n |
| n |
| 1+n |
| ||
1+
|
| n+1 |
| 1+n |
则原式=[f(
| 1 |
| 2014 |
| 1 |
| 2013 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
下列四个交通标志图形中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,已知AC∥BD,OA=OC,则下列结论不成立的是( )
如图,已知AC∥BD,OA=OC,则下列结论不成立的是( )| A、∠B=∠C |
| B、∠A=∠D |
| C、∠AOC=∠BOD |
| D、OA=OB |
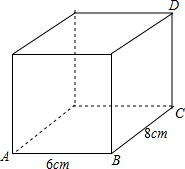 如图所示,一个长方体的纸盒,它的长、宽分别是6cm,8cm,最长能放一根长26cm的木棒,这个纸盒的高应是多少?说明你的理由.
如图所示,一个长方体的纸盒,它的长、宽分别是6cm,8cm,最长能放一根长26cm的木棒,这个纸盒的高应是多少?说明你的理由.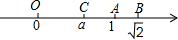 如图,数轴上表示1,
如图,数轴上表示1,