题目内容
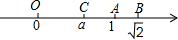 如图,数轴上表示1,
如图,数轴上表示1,| 2 |
考点:实数与数轴
专题:
分析:先求出线段AB的长度,然后根据对称的性质求出a点表示的数,代入式子化简即可.
解答:解:∵数轴上与1、
两个实数对应的点分别为A、B,
∴AB=
-1,
设点C表示的数为x,
∵AC=AB,
∴1-x=
-1,
解可得x=2-
,
即点C所对应的数为2-
.
所以原式=(2-
-2)2-|2-
-1|-(2-
)
=2-(
-1)-2+
=2-
+1-2+
=1.
| 2 |
∴AB=
| 2 |
设点C表示的数为x,
∵AC=AB,
∴1-x=
| 2 |
解可得x=2-
| 2 |
即点C所对应的数为2-
| 2 |
所以原式=(2-
| 2 |
| 2 |
| 2 |
=2-(
| 2 |
| 2 |
| 2 |
| 2 |
点评:此题主要考查了利用数形结合的思想求出数轴两点之间的距离,解决问题的关键是根据已知条件求出a的值,代入化简时要注意括号的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,晚上小亮在路灯下经过,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
如图,晚上小亮在路灯下经过,在小亮由A处径直走到B处这一过程中,他在地上的影子( )| A、逐渐变短 |
| B、先变短后变长 |
| C、逐渐变长 |
| D、先变长后变短 |
-
的相反数等于( )
| 1 |
| 2 |
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
正六边形的中心角为( )
| A、60° | B、90° |
| C、120° | D、150° |
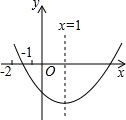 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论: 如图,在△ABC中,∠BAC的平分线AB与BC交于点D,线段AD的垂直平分线与线段BC的延长线交于点F.若BD=3,CF=4,则CD=
如图,在△ABC中,∠BAC的平分线AB与BC交于点D,线段AD的垂直平分线与线段BC的延长线交于点F.若BD=3,CF=4,则CD=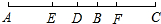 如图,已知线段AB和CD的公共部分BD=
如图,已知线段AB和CD的公共部分BD=