题目内容
3.一次函数y=-x+3的图象上有两点(x1,y1)和(x2,y2),且x1<x2,则y1与y2的大小关系为y1>y2.分析 先根据从一次函数的解析式判断出函数的增减性,再由x1<x2即可得出结论.
解答 解:∵一次函数y=-x+3中,k=-1<0,
∴y随x的增大而减小.
∵x1<x2,
∴y1>y2.
故答案为:y1>y2.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式解答此题的关键.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
11.为了研究吸烟是否对肺癌有影响,某肿瘤研究所随机地抽查了n人,并进行统计分析.结果显示:在吸烟者中患肺癌的比例是2.5%,在不吸烟者中患肺癌的比例是0.5%,吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人.如果设这n人中,吸烟者患肺癌的人数为x,不吸烟者患肺癌的人数为y,根据题意,下面列出的方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x-y=22}\\{x×2.5%+y×0.5%=n}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y=22}\\{\frac{x}{2.5%}+\frac{y}{0.5%}=n}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=22}\\{x×2.5%-y×0.5%=22}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=22}\\{\frac{x}{2.5%}-\frac{y}{0.5%}=22}\end{array}\right.$ |
8.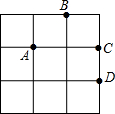 如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )
如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )
 如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )
如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )| A. | A点 | B. | B点 | C. | C点 | D. | D点 |
12. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
①2a+b=0;②b+2c<0;③4a+2b+c<0;④若(0,y1),($\frac{3}{2}$,y2)是抛物线上的两点,那么y1<y2.其中正确的是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①2a+b=0;②b+2c<0;③4a+2b+c<0;④若(0,y1),($\frac{3}{2}$,y2)是抛物线上的两点,那么y1<y2.其中正确的是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
13. 数学课上探究一次函数图象与反比例函数图象有交点时的相关结论:已知直线y=kx+b与x轴、y轴分别交于点C(x,0)、D(0,y),与双曲线y=$\frac{m}{x}$交于点A(x1,y1),B(x2,y2).
数学课上探究一次函数图象与反比例函数图象有交点时的相关结论:已知直线y=kx+b与x轴、y轴分别交于点C(x,0)、D(0,y),与双曲线y=$\frac{m}{x}$交于点A(x1,y1),B(x2,y2).
(1)填空与观察:
(2)发现与验证:
数学学习小组在探究图象交点时发现以下结论:
①x1+x2=x;②y1+y2=y;③当b2+4mk≥0时,两函数图象一定会相交.
你认为以上探究的结论中正确的有①②③(填序号),请选择一个加以证明.
(3)应用与拓展:
连接AO,BO,判断△ACO与△BOD的面积有什么关系,并说明理由.
 数学课上探究一次函数图象与反比例函数图象有交点时的相关结论:已知直线y=kx+b与x轴、y轴分别交于点C(x,0)、D(0,y),与双曲线y=$\frac{m}{x}$交于点A(x1,y1),B(x2,y2).
数学课上探究一次函数图象与反比例函数图象有交点时的相关结论:已知直线y=kx+b与x轴、y轴分别交于点C(x,0)、D(0,y),与双曲线y=$\frac{m}{x}$交于点A(x1,y1),B(x2,y2).(1)填空与观察:
| 函数关系式 | C(x,0) | D(0,y) | A (x1,y1) | B(x2,y2) |
| y=2x+2,y=$\frac{4}{x}$,如图1 | (-1,0) | (0,2) | (1 , 4) | (-2,-2) |
| y=x-3,y=$\frac{10}{x}$,如图2 | (3,0) | (0,-3) | (5,2) | ( -2, -5) |
数学学习小组在探究图象交点时发现以下结论:
①x1+x2=x;②y1+y2=y;③当b2+4mk≥0时,两函数图象一定会相交.
你认为以上探究的结论中正确的有①②③(填序号),请选择一个加以证明.
(3)应用与拓展:
连接AO,BO,判断△ACO与△BOD的面积有什么关系,并说明理由.
 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,3),B(3,1),C(5,4).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,3),B(3,1),C(5,4).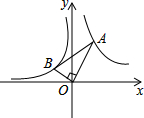 如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,tanA=$\frac{1}{3}$,则k的值为-$\frac{2}{9}$.
如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,tanA=$\frac{1}{3}$,则k的值为-$\frac{2}{9}$.