题目内容
14.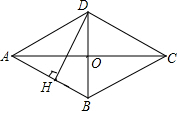 如图,四边形ABCD是菱形,AC=24,BD=10,DH⊥AB于点H,则线段BH的长为$\frac{50}{13}$.
如图,四边形ABCD是菱形,AC=24,BD=10,DH⊥AB于点H,则线段BH的长为$\frac{50}{13}$.
分析 直接利用菱形的性质得出AO,DO的长,再利用三角形面积以及勾股定理得出答案.
解答 解:∵四边形ABCD是菱形,AC=24,BD=10,
∴AO=12,OD=5,AC⊥BD,
∴AD=AB=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
∵DH⊥AB,
∴AO×BD=DH×AB,
∴12×10=13×DH,
∴DH=$\frac{120}{13}$,
∴BH=$\sqrt{1{0}^{2}-(\frac{120}{13})^{2}}$=$\frac{50}{13}$.
故答案为:$\frac{50}{13}$.
点评 此题主要考查了菱形的性质以及勾股定理,正确得出DH的长是解题关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
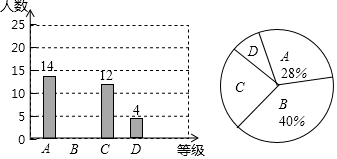
4. 某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
各部门人数及每人所创年利润统计表
(1)①在扇形图中,C部门所对应的圆心角的度数为108°
②在统计表中,b=9,c=6
(2)求这个公司平均每人所创年利润.
 某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图各部门人数及每人所创年利润统计表
| 部门 | 员工人数 | 每人所创的年利润/万元 |
| A | 5 | 10 |
| B | b | 8 |
| C | c | 5 |
②在统计表中,b=9,c=6
(2)求这个公司平均每人所创年利润.
5. 如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
 如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )| A. | ∠1=∠3 | B. | ∠2+∠4=180° | C. | ∠1=∠4 | D. | ∠3=∠4 |
2. 如图,BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠1的度数为( )
如图,BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠1的度数为( )
 如图,BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠1的度数为( )
如图,BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠1的度数为( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
9. 如图,直线a∥b,直线c与直线a,b分别交于点D,E,射线DF⊥直线c,则图中与∠1互余的角有( )
如图,直线a∥b,直线c与直线a,b分别交于点D,E,射线DF⊥直线c,则图中与∠1互余的角有( )
 如图,直线a∥b,直线c与直线a,b分别交于点D,E,射线DF⊥直线c,则图中与∠1互余的角有( )
如图,直线a∥b,直线c与直线a,b分别交于点D,E,射线DF⊥直线c,则图中与∠1互余的角有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
19.下列图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
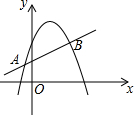 如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是x<-1或x>4.
如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是x<-1或x>4.