题目内容
 正方形ABCD中,E是BD上一点,AE的延长线交CD于F,交BC的延长线于G,M是FG的中点.
正方形ABCD中,E是BD上一点,AE的延长线交CD于F,交BC的延长线于G,M是FG的中点.①求证:∠1=∠2;
②求证:EC⊥MC.
③试问当∠2等于多少度时,△ECG为等腰三角形?请说明理由.
考点:正方形的性质,全等三角形的判定与性质,等腰三角形的判定
专题:
分析:①根据正方形对角线平分一组对角线可得∠ADE=∠CDE,然后利用“边角边”证明△ADE和△CDE全等,根据全等三角形对应角相等可得∠1=∠2;
②根据直角三角形斜边上的中线等于斜边的一半可得MC=MF,再根据等边对等角可得∠MCF=∠MFC,然后求出∠2+∠MCF=90°,最后根据垂直的定义证明;
③根据等边对等角可得∠3=∠G,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠CFG=2∠2,然后根据三角形的内角和定理列出方程求解即可.
②根据直角三角形斜边上的中线等于斜边的一半可得MC=MF,再根据等边对等角可得∠MCF=∠MFC,然后求出∠2+∠MCF=90°,最后根据垂直的定义证明;
③根据等边对等角可得∠3=∠G,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠CFG=2∠2,然后根据三角形的内角和定理列出方程求解即可.
解答:①证明:在正方形ABCD中,∠ADE=∠CDE,AD=CD,
在△ADE和△CDE中,
,
∴△ADE≌△CDE(SAS),
∴∠1=∠2;
②∵M是FG的中点,
∴MC=MF,
∴∠MCF=∠MFC,
∵AD∥BC,
∴∠1=∠G,
∵∠G+∠MFC=90°,
∴∠2+∠MCF=90°,
∴EC⊥MC;
③解:∠2=30°时,△ECG为等腰三角形.
∵△ECG为等腰三角形,
∴∠3=∠G,
∵∠1=∠2,∠1=∠G,
∴∠2=∠G,
由三角形的外角性质,∠CFG=∠2+∠3=2∠2,
在Rt△CFG中,∠G+∠CFG=90°,
∴∠2+2∠2=90°,
解得∠2=30°,
故∠2=30°时,△ECG为等腰三角形.
在△ADE和△CDE中,
|
∴△ADE≌△CDE(SAS),
∴∠1=∠2;
②∵M是FG的中点,
∴MC=MF,
∴∠MCF=∠MFC,
∵AD∥BC,
∴∠1=∠G,
∵∠G+∠MFC=90°,
∴∠2+∠MCF=90°,

∴EC⊥MC;
③解:∠2=30°时,△ECG为等腰三角形.
∵△ECG为等腰三角形,
∴∠3=∠G,
∵∠1=∠2,∠1=∠G,
∴∠2=∠G,
由三角形的外角性质,∠CFG=∠2+∠3=2∠2,
在Rt△CFG中,∠G+∠CFG=90°,
∴∠2+2∠2=90°,
解得∠2=30°,
故∠2=30°时,△ECG为等腰三角形.
点评:本题考查了正方形的性质,全等三角形的判定与性质,等腰三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并确定出全等的三角形是解题的关键.

练习册系列答案
相关题目
某种感冒病毒的直径是0.00000012米,用科学记数法表示为( )米.
| A、1.2×10-7 |
| B、0.12×10-7 |
| C、1.2×10-6 |
| D、0.12×10-6 |
 已知∠α,利用尺规作∠AOB,使∠AOB=2∠α,请写出作法并作出图形(保留作图痕迹).
已知∠α,利用尺规作∠AOB,使∠AOB=2∠α,请写出作法并作出图形(保留作图痕迹).


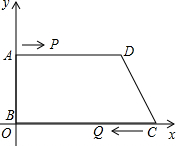 如图,直角梯形ABCD放在平面直角坐标系中,A(0,5),B(0,0),C(26,0),D(24,5)动点P,从A开始沿AD边向D以1cm/s的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B运动.P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts,问:
如图,直角梯形ABCD放在平面直角坐标系中,A(0,5),B(0,0),C(26,0),D(24,5)动点P,从A开始沿AD边向D以1cm/s的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B运动.P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts,问: