题目内容
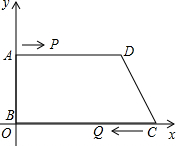如图，直角梯形ABCD放在平面直角坐标系中，A（0，5），B（0，0），C（26，0），D（24，5）动点P，从A开始沿AD边向D以1cm/s的速度运动，动点Q从点C开始沿CB以3cm/s的速度向点B运动．P、Q同时出发，当其中一点到达顶点时，另一点也随之停止运动，设运动时间为ts，问：（1）当t为何值时，四边形PQCD是平行四边形？
（2）当t为何值时，四边形PQCD为等腰梯形．
考点：直角梯形,平行四边形的判定,等腰梯形的判定
专题：动点型
分析：（1）画出图形，根据平行四边形的判定得出当DP=CQ时，四边形PQCD是平行四边形，得出方程，求出即可；
（2）画出图形，根据等腰三角形的判定得出当QN=MC时，根据勾股定理求出PQ=CD，即得出等腰梯形PQCD，得出方程，求出即可．
（2）画出图形，根据等腰三角形的判定得出当QN=MC时，根据勾股定理求出PQ=CD，即得出等腰梯形PQCD，得出方程，求出即可．
解答：解：（1）如图1，
∵A（0，5），B（0，0），C（26，0），D（24，5），
∴AB=5，AD=24，BC=26，
∵AD∥BC，
∴当DP=CQ时，四边形PQCD是平行四边形，
即24-t=3t，
解得：t=6，
即当t=6s时，四边形PQCD是平行四边形；
（2）如图2，
过P作PN⊥BC于N，过D作DM⊥BC于M，
∵PN=DM=AB=5，
∴当NQ=MC时，四边形PQCD是等腰梯形，
∴24-t=3t-2×（26-24），
解得：t=7，
即当t=7s时，四边形PQCD为等腰梯形．
∵A（0，5），B（0，0），C（26，0），D（24，5），
∴AB=5，AD=24，BC=26，
∵AD∥BC，
∴当DP=CQ时，四边形PQCD是平行四边形，
即24-t=3t，
解得：t=6，
即当t=6s时，四边形PQCD是平行四边形；
（2）如图2，
过P作PN⊥BC于N，过D作DM⊥BC于M，
∵PN=DM=AB=5，
∴当NQ=MC时，四边形PQCD是等腰梯形，
∴24-t=3t-2×（26-24），
解得：t=7，
即当t=7s时，四边形PQCD为等腰梯形．
点评：本题考查了坐标与图形性质，勾股定理，等腰梯形的判定，平行四边形的判定的应用，解此题的关键是能根据题意得出方程，题目是一道比较好的题目，难度适中．
练习册系列答案
阅读快车系列答案
相关题目
如图，有一块不规则的菜地ABCD，已知∠ABC=90°，AB=3m，BC=4m，AD=12m，CD=13m，求这块菜地的面积．
正方形ABCD中，E是BD上一点，AE的延长线交CD于F，交BC的延长线于G，M是FG的中点．
实数a，b，c是数轴上三点A，B，C所对应的数，如图，化简：