题目内容
1. 如图,AB为⊙O直径,C为⊙O上一点,点D是$\widehat{BC}$的中点,DE⊥AC于E,DF⊥AB于F.
如图,AB为⊙O直径,C为⊙O上一点,点D是$\widehat{BC}$的中点,DE⊥AC于E,DF⊥AB于F.(1)判断DE与⊙O的位置关系,并证明你的结论;
(2)若OF=4,求AC的长度.
分析 (1)先连接OD、AD,根据点D是$\widehat{BC}$的中点,得出∠DAO=∠DAC,进而根据内错角相等,判定OD∥AE,最后根据DE⊥OD,得出DE与⊙O相切;
(2)先连接BC交OD于H,延长DF交⊙O于G,根据垂径定理推导可得OH=OF=4,再根据AB是直径,推出OH是△ABC的中位线,进而得到AC的长是OH长的2倍.本题也可以过O作OM⊥AC于M,根据全等三角形的性质以及垂径定理进行求解.
解答 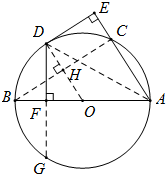 解:(1)DE与⊙O相切.
解:(1)DE与⊙O相切.
证明:连接OD、AD,
∵点D是$\widehat{BC}$的中点,
∴$\widehat{BD}$=$\widehat{CD}$,
∴∠DAO=∠DAC,
∵OA=OD,
∴∠DAO=∠ODA,
∴∠DAC=∠ODA,
∴OD∥AE,
∵DE⊥AC,
∴DE⊥OD,
∴DE与⊙O相切.
(2)解法1:连接BC交OD于H,延长DF交⊙O于G,
由垂径定理可得:OH⊥BC,$\widehat{BG}$=$\widehat{BD}$=$\widehat{DC}$,
∴$\widehat{DG}$=$\widehat{BC}$,
∴DG=BC,
∴弦心距OH=OF=4,
∵AB是直径,
∴BC⊥AC,
又∵OH∥AC,
∴OH是△ABC的中位线,
∴AC=2OH=8.
解法2:如图,过O作OM⊥AC于M,则四边形DOME是矩形,
∴∠DOM=90°,
又∵DF⊥AB,
∴∠FDO+∠FOD=∠MOA+∠FOD=90°,
∴∠FDO=∠MOA,
在△FDO和△MOA中,
$\left\{\begin{array}{l}{∠DFO=∠OMA=90°}\\{∠FDO=∠MOA}\\{DO=OA}\end{array}\right.$,
∴△FDO≌△MOA(AAS),
∴AM=OF=4,
又∵OM⊥AC,
∴AC=2AM=8.
点评 本题主要考查了直线与圆的位置关系以及垂径定理的运用,在判定一条直线为圆的切线时,当已知条件中明确指出直线与圆有公共点时,通常连接过该公共点的半径,证明该半径垂直于这条直线.本题也可以根据△ODF与△ABC相似,求得AC的长.

 走进文言文系列答案
走进文言文系列答案①-4>-2;②若a=b,则a2=b2;③同角的余角相等;④两直线平行,同位角相等
其中,真命题有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| 运行区间 | 票价 | ||
| 起点站 | 终点站 | 一等座 | 二等座 |
| 都匀 | 桂林 | 95(元) | 60(元) |
(2)由于各种原因,二等座单程火车票只能买x张(x<参加社会实践的总人数),其余的须买一等座单程火车票,在保证所有人员都有座位的前提下,请你设计最经济的购票方案,并写出购买单程火车票的总费用y与x之间的函数关系式.
(3)在(2)的方案下,请求出当x=30时,购买单程火车票的总费用.
| A. | 24 | B. | 48 | C. | 96 | D. | 192 |
 如图,矩形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm,当沿AE折叠时,顶点D落在BC边上的点F处,试求CE的长.
如图,矩形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm,当沿AE折叠时,顶点D落在BC边上的点F处,试求CE的长.