题目内容
8.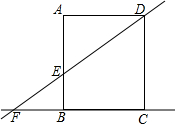 如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6且AE=2EB.则圆心在直线BC上,且与直线DE、AB都相切的⊙O的半径长为$\frac{3}{2}$或6.
如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6且AE=2EB.则圆心在直线BC上,且与直线DE、AB都相切的⊙O的半径长为$\frac{3}{2}$或6.
分析 分两种情况讨论:若⊙O1与直线DE、AB都相切,且圆心O1在AB的左侧,过点O1作O1G1⊥DF于G1,若⊙O2与直线DE、AB都相切,且圆心O2在AB的右侧,过点O2作O2G2⊥DF于G2,求出即可.
解答 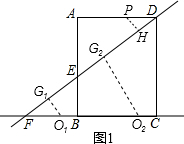 解:∵AD∥BC,
解:∵AD∥BC,
∴△EBF∽△EAD,
∴$\frac{EF}{10}$=$\frac{3}{6}$=$\frac{BF}{8}$,
∴EF=5,BF=4,
如图1,若⊙O1与直线DE、AB都相切,且圆心O1在AB的左侧,过点O1作O1G1⊥DF于G1,
则可设O1G1=O1B=r1,
∵S△EO1F+S△EBO1=S△EBF,
∴$\frac{1}{2}$r1×5+$\frac{1}{2}$r1×3=$\frac{1}{2}$×3×4,
解得:r1=$\frac{3}{2}$,
若⊙O2与直线DE、AB都相切,且圆心O2在AB的右侧,过点O2作O2G2⊥DF于G2,
则可设O2G2=O2B=r2,
∵S△FO2D=$\frac{1}{2}$FO2×DC=$\frac{1}{2}$DF×O2G2,
∴$\frac{1}{2}$×(4+r2)×(6+3)=$\frac{1}{2}$×(10+5)×r2,
解得:r2=6,
即满足条件的圆的半径为$\frac{3}{2}$或6;
故答案为:$\frac{3}{2}$或6.
点评 此题主要考查了圆的综合应用以及切线的性质以及相似三角形的判定与性质等知识,利用分类讨论得出是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.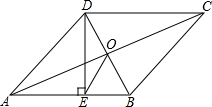 如图,菱形ABCD中,O是对角线AC、BD的交点,DE⊥AB,E是垂足,DE=3,EB=1,则tan∠AOE=( )
如图,菱形ABCD中,O是对角线AC、BD的交点,DE⊥AB,E是垂足,DE=3,EB=1,则tan∠AOE=( )
 如图,菱形ABCD中,O是对角线AC、BD的交点,DE⊥AB,E是垂足,DE=3,EB=1,则tan∠AOE=( )
如图,菱形ABCD中,O是对角线AC、BD的交点,DE⊥AB,E是垂足,DE=3,EB=1,则tan∠AOE=( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
20.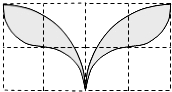 如图,小方格都是边长为的正方形,则以格点为圆心,半径为和2的两种弧围成的“叶状”阴影图案的面积为( )
如图,小方格都是边长为的正方形,则以格点为圆心,半径为和2的两种弧围成的“叶状”阴影图案的面积为( )
 如图,小方格都是边长为的正方形,则以格点为圆心,半径为和2的两种弧围成的“叶状”阴影图案的面积为( )
如图,小方格都是边长为的正方形,则以格点为圆心,半径为和2的两种弧围成的“叶状”阴影图案的面积为( )| A. | 4π-2 | B. | 2π-2 | C. | 4π-4 | D. | 2π-4 |
 如图,E、A、C、F在同一条直线上,AD∥BC,AD=BC,AE=CF,求证:ED∥BF.
如图,E、A、C、F在同一条直线上,AD∥BC,AD=BC,AE=CF,求证:ED∥BF.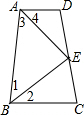 如图,AD∥BC,∠ABC和∠BAD的平分线相交于点E,过E的直线分别交AD、BC于D、C,试问:AB=AD+BC吗?说明你的理由.
如图,AD∥BC,∠ABC和∠BAD的平分线相交于点E,过E的直线分别交AD、BC于D、C,试问:AB=AD+BC吗?说明你的理由.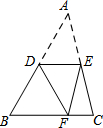 如图,△ABC的中位线DE=5,把△ABC沿DE折叠,使点A落在边BC上的点F处,且AF=8,则BC=10,△ABC的面积为40.
如图,△ABC的中位线DE=5,把△ABC沿DE折叠,使点A落在边BC上的点F处,且AF=8,则BC=10,△ABC的面积为40.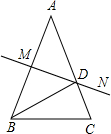 如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D、交AB于点M.下列结论:①BD是∠ABC的平分线;②△BCD是等腰三角形;③∠BDC=72°.正确的结论有几个( )
如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D、交AB于点M.下列结论:①BD是∠ABC的平分线;②△BCD是等腰三角形;③∠BDC=72°.正确的结论有几个( ) 如图,在?ABCD中,AC⊥AB,∠ABD=30°,AC交BD于O,AO=1,则BC的长为$\sqrt{7}$.
如图,在?ABCD中,AC⊥AB,∠ABD=30°,AC交BD于O,AO=1,则BC的长为$\sqrt{7}$.