题目内容
3.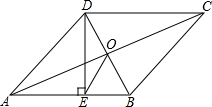 如图,菱形ABCD中,O是对角线AC、BD的交点,DE⊥AB,E是垂足,DE=3,EB=1,则tan∠AOE=( )
如图,菱形ABCD中,O是对角线AC、BD的交点,DE⊥AB,E是垂足,DE=3,EB=1,则tan∠AOE=( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
分析 由菱形ABCD中,DE⊥AB,根据直角三角形斜边的中线等于斜边的一半,可得OE=OB,继而求得∠ADB=∠ABD=∠OEB,则可得∠BAD=∠BOE,继而证得∠AOE=∠ADE,再设AD=x,则AE=AB-B=x-1,由勾股定理,即可求得答案.
解答 解:∵四边形ABCD是菱形,
∴AD=AB,OB=OD,AC⊥BD,OB=OD,
∴OE=OB=$\frac{1}{2}$BD,
∴∠OBE=∠OEB,
∵AB=AD,
∴∠OBE=∠ADB,
∴∠BAD=∠BOE,
∵∠BAD+∠ADE=90°,∠BOE+∠AOE=90°,
∴∠AOE=∠ADE,
设AD=x,则AE=AB-B=x-1,
∵DE⊥AB,DE=3,
∴AD2=AE2+DE2,
∴x2=32+(x-1)2,
解得:x=5,
∴AD=AB=5,AE=4,
∴tan∠AOE=tan∠ADE=$\frac{AE}{DE}$=$\frac{4}{3}$.
故选D.
点评 此题考查了菱形的性质、勾股定理以及直角三角形斜边的中线的性质.注意证得∠AOE=∠ADE是关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
12.在下列各电视台的台标图案中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
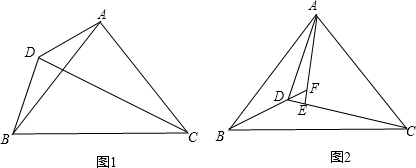
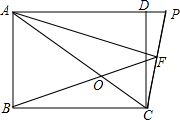 已知矩形ABCD中,AF为∠DAC的角平分线,CP⊥AF于点F,且交AD的延长线于P.连接BF交对角线AC于点O.
已知矩形ABCD中,AF为∠DAC的角平分线,CP⊥AF于点F,且交AD的延长线于P.连接BF交对角线AC于点O.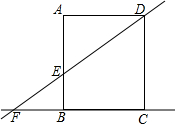 如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6且AE=2EB.则圆心在直线BC上,且与直线DE、AB都相切的⊙O的半径长为$\frac{3}{2}$或6.
如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6且AE=2EB.则圆心在直线BC上,且与直线DE、AB都相切的⊙O的半径长为$\frac{3}{2}$或6.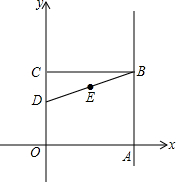 如图,O是坐标原点,矩形OABC的顶点A在z轴的正半轴上,点C在y轴的正半轴上,点D在边OC上,且点B(6,5),tan∠CBD=$\frac{1}{3}$.
如图,O是坐标原点,矩形OABC的顶点A在z轴的正半轴上,点C在y轴的正半轴上,点D在边OC上,且点B(6,5),tan∠CBD=$\frac{1}{3}$.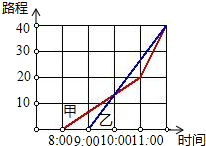 如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答:
如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答: