题目内容
 如图,AB是⊙O的直径,D是⊙O上一点,过点A的切线与CD的延长线相交于点C,BD的延长线交AC于E,△ACD与△DCE相似吗?为什么?
如图,AB是⊙O的直径,D是⊙O上一点,过点A的切线与CD的延长线相交于点C,BD的延长线交AC于E,△ACD与△DCE相似吗?为什么?考点:相似三角形的判定,切线的性质
专题:常规题型
分析:根据切线的性质得BA⊥AC,则∠BAD+∠DAC=90°,再根据圆周角定理得∠B+∠BAD=90°,则∠B=∠DAC,加上∠B=∠ODB,∠ODB=∠CDE,易得∠CDE=DAE,于是可根据有两组角对应相等的两个三角形相似得到△ACD∽△DCE.
解答:解:△ACD与△DCE相似.理由如下:
∵AC为⊙O的切线,
∴BA⊥AC,
∴∠BAD+∠DAC=90°,
∵AB为直径,
∴∠ADB=90°,
∴∠B+∠BAD=90°,
∴∠B=∠DAC,
∵OB=OD,
∴∠B=∠ODB,
而∠ODB=∠CDE,
∴∠B=∠CDE,
∠而∠ECD=∠DCA,
∴△ACD∽△DCE.
∵AC为⊙O的切线,
∴BA⊥AC,
∴∠BAD+∠DAC=90°,
∵AB为直径,
∴∠ADB=90°,
∴∠B+∠BAD=90°,
∴∠B=∠DAC,
∵OB=OD,
∴∠B=∠ODB,
而∠ODB=∠CDE,
∴∠B=∠CDE,
∠而∠ECD=∠DCA,
∴△ACD∽△DCE.
点评:本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了圆周角定理和切线的性质.

练习册系列答案
相关题目
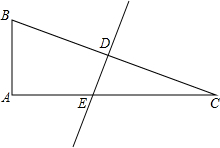 如图,在△ABC中,AB=6,AC=8,BC=10,现将它折叠,使B点与C点重合,求折痕DE的长.
如图,在△ABC中,AB=6,AC=8,BC=10,现将它折叠,使B点与C点重合,求折痕DE的长.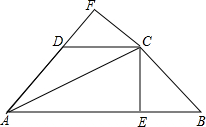 如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD, 如图,兴华中学有两块紧挨着的边长分别为a,b的正方形空地,为了美化校园,现打算在图中阴影部分种植草皮,求所要种植草皮的面积.
如图,兴华中学有两块紧挨着的边长分别为a,b的正方形空地,为了美化校园,现打算在图中阴影部分种植草皮,求所要种植草皮的面积.