题目内容
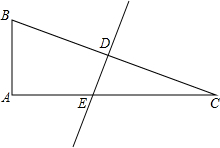 如图,在△ABC中,AB=6,AC=8,BC=10,现将它折叠,使B点与C点重合,求折痕DE的长.
如图,在△ABC中,AB=6,AC=8,BC=10,现将它折叠,使B点与C点重合,求折痕DE的长.考点:翻折变换(折叠问题)
专题:
分析:首先根据勾股定理的逆定理证明△BAC直角三角形,然后证明∠CDE=∠A,进而证明△CDE∽△CAB,于是求出DE的长.
解答:解:在△ABC中,AB2+AC2=62+82=100,
BC2=102=100,
∴AB2+AC2=BC2,
∴∠A=90°,
∵B与C重合,
∴DE垂直平分BC,
∴CD=
BC=
×10=5,∠CDE=90°,
∴∠CDE=∠A,
∵∠C=∠C,
∴△CDE∽△CAB,
∴
=
,
∴
=
,
∴DE=
.
BC2=102=100,
∴AB2+AC2=BC2,
∴∠A=90°,
∵B与C重合,
∴DE垂直平分BC,
∴CD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CDE=∠A,
∵∠C=∠C,
∴△CDE∽△CAB,
∴
| DE |
| AB |
| CD |
| CA |
∴
| DE |
| 6 |
| 5 |
| 8 |
∴DE=
| 15 |
| 4 |
点评:本题主要考查了翻折变换的知识,解答本题的关键是熟练利用勾股定理的逆定理以及证明△CDE∽△CAB,此题难度不大,是一道中考常考试题.

练习册系列答案
相关题目
 如图,以Rt△ABC的斜边BC为斜边在△ABC的同侧作等腰Rt△BCD,连接AD,过D作DE⊥AD交AC于E,AB=1,AD=
如图,以Rt△ABC的斜边BC为斜边在△ABC的同侧作等腰Rt△BCD,连接AD,过D作DE⊥AD交AC于E,AB=1,AD= (1)如图1,DE∥FG∥BC,AD=DF=2FB,那么AE、EG、GC有什么关系?
(1)如图1,DE∥FG∥BC,AD=DF=2FB,那么AE、EG、GC有什么关系? 如图,AB是⊙O的直径,D是⊙O上一点,过点A的切线与CD的延长线相交于点C,BD的延长线交AC于E,△ACD与△DCE相似吗?为什么?
如图,AB是⊙O的直径,D是⊙O上一点,过点A的切线与CD的延长线相交于点C,BD的延长线交AC于E,△ACD与△DCE相似吗?为什么?