题目内容
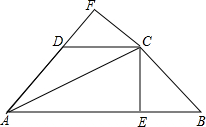 如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,(1)求证:△BCE≌△DCF;
(2)若∠BAD=50°,求∠DCB的度数;
(3)若AB=21,AD=9,BC=CD=10,求AC的长.
考点:全等三角形的判定与性质,角平分线的性质,勾股定理
专题:
分析:(1)易证∠CFD=90°,∠CEB=90°,CE=CF,即可证明Rt△BCE≌Rt△DCF;
(2)由(1)结论可得∠DCF=∠BCE,即可求得∠DCB=∠FCE,易求∠FCE=130°,即可解题;
(3)易求CF=CE,即可证明RT△ACF≌RT△ACE,可得AF=AE,根据DF=BE,即可求得AE的长,可求得BE的长,根据勾股定理即可求得CE的长,再根据勾股定理即可求得AC的长,即可解题.
(2)由(1)结论可得∠DCF=∠BCE,即可求得∠DCB=∠FCE,易求∠FCE=130°,即可解题;
(3)易求CF=CE,即可证明RT△ACF≌RT△ACE,可得AF=AE,根据DF=BE,即可求得AE的长,可求得BE的长,根据勾股定理即可求得CE的长,再根据勾股定理即可求得AC的长,即可解题.
解答:(1)证明:∵AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,
∴∠CFD=90°,∠CEB=90°,CE=CF,
在Rt△BCE和Rt△DCF中,
,
∴Rt△BCE≌Rt△DCF(HL);
(2)解:∵Rt△BCE≌Rt△DCF,
∴∠DCF=∠BCE,
∵∠F=∠AEC=90°,∠BAD=50°,
∴∠FCE=130°,
∵∠DCB=∠DCE+∠BCE=∠DCE+∠DCF=∠FCE,
即∠DCB=∠FCE=130°.
(3)解:∵AC平分∠BAD,CF⊥AF,CE⊥AE,
∴CF=CE,
在RT△ACF和RT△ACE中,
,
∴RT△ACF≌RT△ACE(HL),
∴AF=AE,
∵Rt△BCE≌Rt△DCF,
∴DF=BE,
∴AF+AE=AE+BE+AF-DF=AB+AD=30,
∴AE=15,
∴BE=6,
∵CE=
=8,
∴AC=
=17.
答:AC的长为17.
∴∠CFD=90°,∠CEB=90°,CE=CF,
在Rt△BCE和Rt△DCF中,
|
∴Rt△BCE≌Rt△DCF(HL);
(2)解:∵Rt△BCE≌Rt△DCF,
∴∠DCF=∠BCE,
∵∠F=∠AEC=90°,∠BAD=50°,
∴∠FCE=130°,
∵∠DCB=∠DCE+∠BCE=∠DCE+∠DCF=∠FCE,
即∠DCB=∠FCE=130°.
(3)解:∵AC平分∠BAD,CF⊥AF,CE⊥AE,
∴CF=CE,
在RT△ACF和RT△ACE中,
|
∴RT△ACF≌RT△ACE(HL),
∴AF=AE,
∵Rt△BCE≌Rt△DCF,
∴DF=BE,
∴AF+AE=AE+BE+AF-DF=AB+AD=30,
∴AE=15,
∴BE=6,
∵CE=
| BC2-BE2 |
∴AC=
| AE2+CE2 |
答:AC的长为17.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证Rt△BCE≌Rt△DCF和RT△ACF≌RT△ACE是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
 如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC.
如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC. (1)如图1,DE∥FG∥BC,AD=DF=2FB,那么AE、EG、GC有什么关系?
(1)如图1,DE∥FG∥BC,AD=DF=2FB,那么AE、EG、GC有什么关系?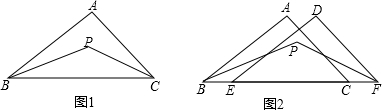
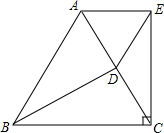
 如图,AB是⊙O的直径,D是⊙O上一点,过点A的切线与CD的延长线相交于点C,BD的延长线交AC于E,△ACD与△DCE相似吗?为什么?
如图,AB是⊙O的直径,D是⊙O上一点,过点A的切线与CD的延长线相交于点C,BD的延长线交AC于E,△ACD与△DCE相似吗?为什么? 根据下列语句画出图形并计算.
根据下列语句画出图形并计算.