题目内容
 如图,在△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,求∠CAF的度数.
如图,在△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,求∠CAF的度数.考点:线段垂直平分线的性质,等腰三角形的性质
专题:
分析:先根据线段垂直平分线的性质及BE⊥AC得出△ABE是等腰直角三角形,再由等腰三角形的性质得出∠ABC的度数,由直角三角形的性质来求∠CAF的度数.
解答:解:∵DE垂直平分AB,
∴AE=BE,
∵BE⊥AC,
∴△ABE是等腰直角三角形,
∴∠BAC=∠ABE=45°,
又∵AB=AC,
∴∠ABC=
(180°-∠BAC)=
(180°-45°)=67.5°,
又∵AF⊥BC,
∴∠AFC=90°,
∴∠CAF=90°-67.5°=22.5°.
即∠CAF=22.5°.
∴AE=BE,
∵BE⊥AC,
∴△ABE是等腰直角三角形,
∴∠BAC=∠ABE=45°,
又∵AB=AC,
∴∠ABC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵AF⊥BC,
∴∠AFC=90°,
∴∠CAF=90°-67.5°=22.5°.
即∠CAF=22.5°.
点评:本题考查的是线段垂直平分线的性质,熟知垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列各数:0.5、
、-0.03745、
、
、1-
,其中无理数的个数为( )
| 3 | 125 |
| 1 |
| 3 |
| 0.12 |
| 5 |
| A、2 | B、3 | C、4 | D、5 |

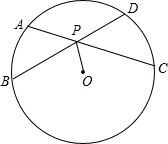 如图,AC、BD为圆O的两条弦,AC、BD相交于点P,连结OP,若OP平分∠BPC,求证:AC=BD.
如图,AC、BD为圆O的两条弦,AC、BD相交于点P,连结OP,若OP平分∠BPC,求证:AC=BD. 如图,P为正△ABC内的一点,PA=2,PB=4,PC=2
如图,P为正△ABC内的一点,PA=2,PB=4,PC=2 已知如图,AD∥BC,E为DC上一点,∠1=∠2,∠3=∠4.求证:CE=ED.
已知如图,AD∥BC,E为DC上一点,∠1=∠2,∠3=∠4.求证:CE=ED.