题目内容
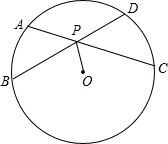 如图,AC、BD为圆O的两条弦,AC、BD相交于点P,连结OP,若OP平分∠BPC,求证:AC=BD.
如图,AC、BD为圆O的两条弦,AC、BD相交于点P,连结OP,若OP平分∠BPC,求证:AC=BD.考点:垂径定理,角平分线的性质,勾股定理
专题:证明题
分析:过O作OM⊥BD于M,ON⊥AC于N,连接OC、OB,根据垂径定理求出AC=2CN,BD=2BM,根据角平分线性质求出OM=ON,根据勾股定理求出BM=CN,即可得出答案.
解答:证明: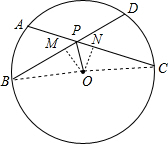
过O作OM⊥BD于M,ON⊥AC于N,连接OC、OB,
∵OP平分∠BPC,
∴OM=ON,
在Rt△BMO和Rt△CON中,由勾股定理得:BM2=0B2-OM2,CN2=OC2-ON2,
∵OB=OC,
∴CN=BM,
由垂径定理得:BD=2BM,AC=2CN,
∴AC=BD.

过O作OM⊥BD于M,ON⊥AC于N,连接OC、OB,
∵OP平分∠BPC,
∴OM=ON,
在Rt△BMO和Rt△CON中,由勾股定理得:BM2=0B2-OM2,CN2=OC2-ON2,
∵OB=OC,
∴CN=BM,
由垂径定理得:BD=2BM,AC=2CN,
∴AC=BD.
点评:本题考查了角平分线性质,勾股定理,垂径定理的应用,主要考查学生的推理能力.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
如果两个数的绝对值相等,那么这两个数是( )
| A、互为相反数 | B、相等 |
| C、积为0 | D、互为相反数或相等 |
 如图:在△ABC中,∠BAC=100°,∠ACB=20°,CE是∠ACB的角平分线,D是BC上一点,若∠DAC=20°,求∠CED的度数.
如图:在△ABC中,∠BAC=100°,∠ACB=20°,CE是∠ACB的角平分线,D是BC上一点,若∠DAC=20°,求∠CED的度数. 如图,在△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,求∠CAF的度数.
如图,在△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,求∠CAF的度数.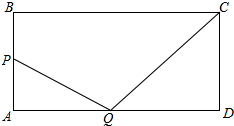 如图,矩形ABCD,AB=6cm,AD=12cm,P是AB上的动点,Q是AD上的动点.P以1cm/s的速度从B到A,Q以2cm/s的速度从A到D,P到A(或Q到D)时停止运动.求PQ+QC最小值.
如图,矩形ABCD,AB=6cm,AD=12cm,P是AB上的动点,Q是AD上的动点.P以1cm/s的速度从B到A,Q以2cm/s的速度从A到D,P到A(或Q到D)时停止运动.求PQ+QC最小值. 如图,已知AB=AC,AD⊥BC,垂足为点D,∠BAC=100°,BC=8cm.
如图,已知AB=AC,AD⊥BC,垂足为点D,∠BAC=100°,BC=8cm.