题目内容
(1)如图①,在凹四边形ABCD中,∠ABD与∠ACD的角平分线交于点E,∠A=60°,∠BDC=140°,则∠E= °;
(2)如图②,∠ABD,∠BAC的角平分线交于点E,∠C=40°,∠BDC=150°,求∠AEB的度数;
(3)如图③,∠BAC,∠DBC的角平分线交于点E,则∠B,∠C与∠E之间有怎样的数量关系 .
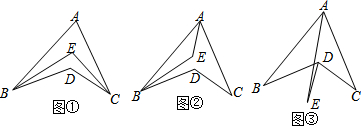
(2)如图②,∠ABD,∠BAC的角平分线交于点E,∠C=40°,∠BDC=150°,求∠AEB的度数;
(3)如图③,∠BAC,∠DBC的角平分线交于点E,则∠B,∠C与∠E之间有怎样的数量关系

考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)连接BC,由三角形内角和定理求出∠ABC+∠ACB的度数,再根据∠BDC=140°求出∠DBC+∠DCB的度数,根据∠ABD与∠ACD的角平分线交于点E求出∠EBD+∠ECD的度数,根据三角形内角和定理即可得出∠E的度数;
(2)延长BD交AC于点F,根据∠BDC是△CDF的外角可求出∠CFD的度数,再根据∠CFD是△ABF的外角可得出∠BAC+∠ABD的度数,进而得出结论;
(3)由三角形的外角性质可知,∠BAC+∠B+∠C=∠BDC,再由角平分线的定义可知∠BAE=∠CAE=
∠BAC,∠BDE=∠CDE=
∠BDC,由∠1=∠B+∠BAE=∠B+
∠BAC即可得出结论.
(2)延长BD交AC于点F,根据∠BDC是△CDF的外角可求出∠CFD的度数,再根据∠CFD是△ABF的外角可得出∠BAC+∠ABD的度数,进而得出结论;
(3)由三角形的外角性质可知,∠BAC+∠B+∠C=∠BDC,再由角平分线的定义可知∠BAE=∠CAE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)连接BC,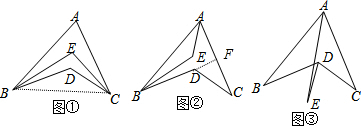
∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∵∠BDC=140°,
∴∠DBC+∠DCB=180°-140°=40°,
∴∠ABD+∠ACD=120°-40°=80°,
∵∠ABD与∠ACD的角平分线交于点E,
∴∠EBD+∠ECD=
×80°=40°,
∴∠EBC+∠ECB=40°+40°=80°,
∴∠E=180°-(∠EBC+∠ECB)=180°-80°=100°.
故答案为:100;
(2)延长BD交AC于点F,
∵∠BDC是△CDF的外角,∠C=40°,∠BDC=150°,
∴∠CFD=∠BDC-∠C=150°-40°=110°,
∵∠CFD是△ABF的外角,
∴∠BAC+∠ABD=∠CFD=110°,
∵∠ABD,∠BAC的角平分线交于点E,
∴∠BAE+∠ABE=
(∠BAC+∠ABD)=
×110°=55°,
∴∠AEB=180°-(∠BAE+∠ABE)=180°-55°=125°;
(3)由三角形的外角性质可知,∠BAC+∠B+∠C=∠BDC,
∵∠BAC,∠BDC的角平分线交于点E,
∴∠BAE=∠CAE=
∠BAC,∠BDE=∠CDE=
∠BDC,
∵∠1=∠B+∠BAE=∠B+
∠BAC,
∴∠B+
∠BAC=∠E+
(∠BAC+∠B+∠C),即∠B-∠C=2∠E.

∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∵∠BDC=140°,
∴∠DBC+∠DCB=180°-140°=40°,
∴∠ABD+∠ACD=120°-40°=80°,
∵∠ABD与∠ACD的角平分线交于点E,
∴∠EBD+∠ECD=
| 1 |
| 2 |
∴∠EBC+∠ECB=40°+40°=80°,
∴∠E=180°-(∠EBC+∠ECB)=180°-80°=100°.
故答案为:100;
(2)延长BD交AC于点F,
∵∠BDC是△CDF的外角,∠C=40°,∠BDC=150°,
∴∠CFD=∠BDC-∠C=150°-40°=110°,
∵∠CFD是△ABF的外角,
∴∠BAC+∠ABD=∠CFD=110°,
∵∠ABD,∠BAC的角平分线交于点E,
∴∠BAE+∠ABE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AEB=180°-(∠BAE+∠ABE)=180°-55°=125°;
(3)由三角形的外角性质可知,∠BAC+∠B+∠C=∠BDC,
∵∠BAC,∠BDC的角平分线交于点E,
∴∠BAE=∠CAE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠1=∠B+∠BAE=∠B+
| 1 |
| 2 |
∴∠B+
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是三角形外角的性质,熟知三角形的一个外角等于和它不相邻的两个内角的和是解答此题的关键.

练习册系列答案
相关题目
 如图,直线AB、CD相交于点O,若∠1+∠2=100°,则∠BOC等于( )
如图,直线AB、CD相交于点O,若∠1+∠2=100°,则∠BOC等于( )| A、130° | B、140° |
| C、150° | D、160° |
 如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )
如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )| A、4 | B、8 | C、12 | D、16 |
 如图,△EDF中,∠EDF=90°,点B是EF的中点,点M在边ED上,过点B作MB的垂线交边DF于N点,求证:BM2+BN2=ME2+NF2.
如图,△EDF中,∠EDF=90°,点B是EF的中点,点M在边ED上,过点B作MB的垂线交边DF于N点,求证:BM2+BN2=ME2+NF2.
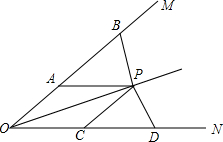 如图,OP平分∠MON,点A与B,点C与D分别在射线OM、ON上,且AB=CD
如图,OP平分∠MON,点A与B,点C与D分别在射线OM、ON上,且AB=CD



 如图,已知AB∥CD,EF⊥AB于E,∠EFG=55°,求∠EGF的度数.
如图,已知AB∥CD,EF⊥AB于E,∠EFG=55°,求∠EGF的度数.