题目内容
12.直角三角板ABC与AFE的形状大小完全相同,且两直角边分别为3和4,先按如图甲所示位置放置放置,再将Rt△AEF绕A点按顺时针方向旋转角α(0°<α<90°),如图乙,AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当四边形ABPF是菱形时,求△AMC的面积.

分析 (1)先由△ABC和△AFE的形状大小完全相同得到AB=AF,∠ABC=∠AFE,再根据旋转的性质得∠BAE=∠FAC=α,于是可利用“ASA”证明△ABM≌△AFN,所以AM=AN;
(2)在Rt△ABC中利用勾股定理计算出BC=5,再由菱形性质得AB∥PF,得到∠ANF=∠BAC=90°,接着根据△ABM≌△AFN得到∠AMB=∠ANF=90°,则可根据面积法计算出AM=$\frac{12}{5}$,然后在Rt△AMC中利用勾股定理计算出MC=$\frac{16}{5}$,最后根据三角形面积公式求解.
解答 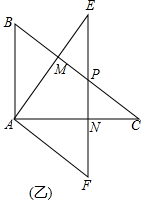 (1)证明:∵△ABC和△AFE的形状大小完全相同,
(1)证明:∵△ABC和△AFE的形状大小完全相同,
∴AB=AF,∠ABC=∠AFE,
∵Rt△AEF绕A点按顺时针方向旋转角α(0°<α<90°),如图乙,
∴∠BAE=∠FAC=α,
在△ABM和△AFN中,
$\left\{\begin{array}{l}{∠ABM=∠AFN}\\{AB=AF}\\{∠BAM=∠FAN}\end{array}\right.$,
∴△ABM≌△AFN(ASA),
∴AM=AN;
(2)在Rt△ABC中,∵AB=3,AC=4,
∴BC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵四边形ABPF是菱形,
∴AB∥PF,
∴∠ANF=∠BAC=90°,
∵△ABM≌△AFN,
∴∠AMB=∠ANF=90°,
∵$\frac{1}{2}$AM•BC=$\frac{1}{2}$AB•AC,
∴AM=$\frac{3×4}{5}$=$\frac{12}{5}$,
在Rt△AMC中,∵AC=4,AM=$\frac{12}{5}$,
∴MC=$\sqrt{{4}^{2}-(\frac{12}{5})^{2}}$=$\frac{16}{5}$,
∴S△AMC=$\frac{1}{2}$AM•MC=$\frac{1}{2}$×$\frac{12}{5}$×$\frac{16}{5}$=$\frac{96}{25}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.旋转有三要素:旋转中心; 旋转方向; 旋转角度.也考查了全等三角形的判定与性质、菱形性质和勾股定理.

| 周数x | 1 | 2 | 3 | 4 |
| 价格y(元/千克) | 2 | 2.2 | 2.4 | 2.6 |
(2)进入9月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y(元/千克)从9月第1周的2.8元/千克下降至第2周的2.4元/千克,且y与周数x的变化情况满足二次函数y=-$\frac{1}{20}$x2+bx+c,请求出9月份y与x的函数关系式;
(3)若8月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=$\frac{1}{4}$x+1.2,9月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=$-\frac{1}{5}$x+2.试问8月份与9月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
(4)若9月份的第2周共销售100吨此种蔬菜.从9月份第3周起,由于受暴雨的影响,此种蔬菜的可供销量将在第2周销量的基础上每周减少a%,政府为稳定蔬菜价格,从外地调运2吨此种蔬菜,刚好满足本地市民的需要,且使此种蔬菜的销售价格比第2周仅上涨0.8a%.若在这一举措下,此种蔬菜在第3周的总销售额与第2周刚好持平,请你参考以下数据,通过计算估算出a的整数值.
(参考数据:372=1369,382=1444,392=1521,402=1600,412=1681)
| A. | a≠0 | B. | a≤4 | C. | a≤4且a≠0 | D. | a<4且a≠0 |
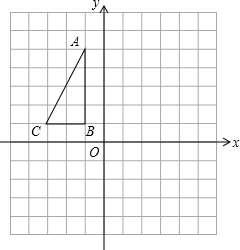 如图,在平面直角坐标系中,ABC的顶点的坐标分别为A(-1,5)、B(-1,1)、C(-3,1).将△ABC向右平移2个单位、再向下平移4个单位得到△A1B1C1;将△ABC绕原点O旋转180°得到△A2B2C2
如图,在平面直角坐标系中,ABC的顶点的坐标分别为A(-1,5)、B(-1,1)、C(-3,1).将△ABC向右平移2个单位、再向下平移4个单位得到△A1B1C1;将△ABC绕原点O旋转180°得到△A2B2C2