题目内容
7．阅读：如图①，已知：正方形ABCD，面积为a，点E、F、G、H分别是AB、BC、CD、DA边的中点，连接AG、BH、CE、DF，求四边形MNPQ的面积．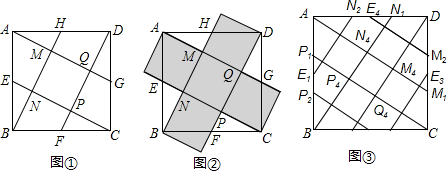
小明提出了如下的解决办法：如图②，分别将△AMH、△BNE、△CPF、△DQG分割并拼补成一个与正方形ABCD面积相等的新图形．请你参考小明同学解决问题的方法，利用图形变换解决下列问题：如图③，在正方形ABCD中，E1、E2、E3、E4分别为AB、BC、CA、DA的中点，P1、P2，Q1、Q2，M1、M2，N1、N2分别为AB、BC、CA、DA的三等分点．
（1）在图③中画出一个和正方形ABCD面积相等的新图形，并用阴影表示（保留画图痕迹）；
（2）图③中四边形P4Q4M4N4的面积为$\frac{1}{13}$a．
分析 （1）根据旋转的性质旋转前后图形面积相等即可得出符合要求的答案；
（2）根据（1）中图形的性质，可以得出阴影部分可以分为13个面积相等的正方形，进而得出答案即可．
解答 解：（1）如图：
（2）∵由（1）题作图知：整个正方形被分成相等的13份，
∴每一份的面积为$\frac{1}{13}$a，
∴图③中四边形P4Q4M4N4的面积为$\frac{1}{13}$a．
点评 此题主要考查了利用旋转设计图案，几何旋转性质得出答案是解题关键．
练习册系列答案
相关题目
18．下列变形不正确的是（ ）
| A． | $\frac{b}{a}=\frac{b•m}{a•m}（m≠0）$ | B． | $\frac{x}{-y}=-\frac{x}{y}$ | C． | $\frac{-x}{-y}=\frac{x}{y}$ | D． | $\frac{{{x^2}+x}}{{{x^2}-1}}=\frac{x}{x+1}$ |
小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的2块带去，就能配一块大小和形状与原来都一样的三角形．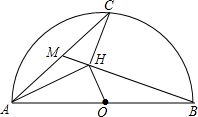
如图，AB是半圆圆O的直径，C是弧AB的中点，M是弦AC的中点，CH⊥BM，垂足为H．求证：CH2=AH•OH．
