题目内容
13．在某校班级网球联赛中，每场比赛都要分出胜负，每队剩一场得3分，负一场得1分，如图某班要在第一轮的25场比赛中至少得42分，那么这个班至少要胜多少场？（ ）| A． | 7 | B． | 8 | C． | 9 | D． | 10 |
分析 设这个班要胜x场，则负（25-x）场，根据题意列出不等式，解不等式即可求出至少要胜几场．
解答 解：设这个班要胜x场，则负（25-x）场，
由题意得，3x+（25-x）≥42，
2x≥17，
解得：x≥8.5，
∵场次x为正整数，
∴x最小=9．
即：这个班至少要胜9场．
故选：C．
点评 本题考查了一元一次不等式的应用，难度一般，解答本题的关键是表示出胜场得分和输场得分并列出不等式．
练习册系列答案
相关题目
3．下列计算，正确的是（ ）
| A． | （x3）2=x5 | B． | x3•x2=x5 | C． | （2x）2=2x3 | D． | （x+1）2=x3+1 |
在?ABCD中，E是AB的中点，F是CD上异于C，D的任意一点，延长CB到G连接FG，已知AB=8，AD=4，∠A=60°
1．若圆柱的底面半径为3cm，母线长为4cm，则这个圆柱的侧面积为（ ）
| A． | 12cm2 | B． | 24cm2 | C． | 12πcm2 | D． | 24πcm2 |
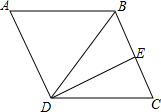如图，平行四边形ABCD中，∠ABC＞∠A，E为BC边的中点，连接BD、ED，∠CDE=30°，∠ADB=∠BDE=2：1，则∠A=60°．