题目内容
4. 在?ABCD中,E是AB的中点,F是CD上异于C,D的任意一点,延长CB到G连接FG,已知AB=8,AD=4,∠A=60°
在?ABCD中,E是AB的中点,F是CD上异于C,D的任意一点,延长CB到G连接FG,已知AB=8,AD=4,∠A=60°(1)试判断△DAE的形状,并说明理由;
(2)求BD的长;
(3)若DF=BG,当DF的长为多少时,△FCG的面积最大,并求出面积的最大值.
分析 (1)先证AE=AD,再由∠A=60°,即可得出△DAE是等边三角形;
(2)先证明△ABD是直角三角形,再根据勾股定理即可得出结果;
(3)作GH⊥AB于H,作DM⊥AB于M,设DF=BG=x,则CF=8-x,先根据锐角三角函数求出DM、BH,即可求出△FCG的面积S是x的二次函数,配方后即可求出结果.
解答 解:(1)△DAE是等边三角形;理由如下:
∵E是AB的中点,
∴AE=BE=$\frac{1}{2}$AB=4,
∴AE=AD,
又∵∠A=60°,
∴△DAE是等边三角形;
(2)∵△DAE是等边三角形,
∴DE=AD=4=$\frac{1}{2}$AB,
∴∠ADB=90°,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$;
(3)作GH⊥AB于H,作DM⊥AB于M,如图所示: 设DF=BG=x,则CF=8-x,
设DF=BG=x,则CF=8-x,
∵四边形ABCD是平行四边形,
∴AD∥CG,
∴∠ABG=∠A=60°,
∴GH=$\frac{\sqrt{3}}{2}$x,
又∵DM=AD•sin60°=2$\sqrt{3}$,
∴△FCG的面积S=$\frac{1}{2}$(8-x)(2$\sqrt{3}$+$\frac{\sqrt{3}}{2}$x)
=-$\frac{\sqrt{3}}{4}$x2+$\sqrt{3}$x+8$\sqrt{3}$
=-$\frac{\sqrt{3}}{4}$(x-2)2+9$\sqrt{3}$,
∵-$\frac{\sqrt{3}}{4}$<0,
∴S有最大值,当x=2,即DF=2时,S的最大值=9$\sqrt{3}$.
点评 本题考查了平行四边形的性质、等边三角形的判定与性质、勾股定理、锐角三角函数以及面积的计算;熟练掌握平行四边形的性质,证明三角形是直角三角形和等边三角形以及求出三角形的高是解决问题的关键.

| A. | $\left\{\begin{array}{l}x=5\\ y=1\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=-5\\ y=-1\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=4\\ y=2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-4\\ y=-2\end{array}\right.$ |
| A. | -1 | B. | 1 | C. | 32014 | D. | -32014 |
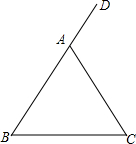 如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.连结BE并延长交∠DAC的平分线AM于点F.
如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.连结BE并延长交∠DAC的平分线AM于点F. 将如图给定的四边形放大一倍,且使位似中心在图形内.
将如图给定的四边形放大一倍,且使位似中心在图形内.