Question

2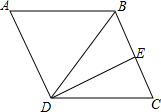．如图，平行四边形ABCD中，∠ABC＞∠A，E为BC边的中点，连接BD、ED，∠CDE=30°，∠ADB=∠BDE=2：1，则∠A=60°．

Answer 1

分析 首先过D作DH⊥AB，过E作EF⊥DC，根据平行四边形的性质可得S_△ADB=S_△DBC，再证明EF=$\frac{1}{2}$ED，根据直角三角形的性质可得EF=$\frac{1}{2}$DE，进而可得DE=DH，根据到角两边的距离相等的点在角的平分线上可得BD平分∠ABC，然后再设∠ADB=2x°，∠BDE=x°，根据平行线的性质可得∠DBC=∠ADB=2x°，∠ABD=∠BDC=（x+30）°，进而可得2x=x+30，再解即可得到x的值，从而可得∠A的度数．

解答 解：过D作DH⊥AB，过E作EF⊥DC，
∵四边形ABCD是平行四边形，
∴S_△ADB=S_△DBC，AB=DC，AB∥CD，AD∥BC，
∵E为BC中点，
∴S_△DEC=$\frac{1}{2}$S_△DBC，
∴S_△DEC=$\frac{1}{2}$S_△ABD，
∴$\frac{1}{2}$AB•DH=$\frac{1}{2}$DC×EF×$\frac{1}{2}$，
∴EF=$\frac{1}{2}$DH，
∵∠EDC=30°，
∴EF=$\frac{1}{2}$ED，
∴DH=DE，
∴BD平分∠ABC，
∵∠ADB=∠BDE=2：1，
∴设∠ADB=2x°，∠BDE=x°，
∴∠BDC=（x+30）°，
∵AB∥CD，AD∥BC，
∴∠DBC=∠ADB=2x°，∠ABD=∠BDC=（x+30）°，
∴2x=x+30，
解得：x=30，
∴∠ADC=30°×3+30°=120°，
∵AB∥CD，
∴∠A+∠ADC=180°，
∴∠A=60°，
故答案为：60°．

点评 此题主要考查了平行四边形的性质，关键是掌握平行四边形的对角线把平行四边形分成两个面积相等的三角形．