题目内容
12. 如图,AB为⊙O的直径,点C是⊙O上一点,BD平分角CBA交⊙O于点D,过点D作直线FE垂直BC,垂足为H,求证:FE是⊙O的切线.
如图,AB为⊙O的直径,点C是⊙O上一点,BD平分角CBA交⊙O于点D,过点D作直线FE垂直BC,垂足为H,求证:FE是⊙O的切线.
分析 连结OD,如图,由BD平分∠CBA得到∠1=∠2,加上∠1=∠3,则∠2=∠3,于是可判断OD∥BH,由于BH⊥EF,所以OD⊥EF,然后根据切线的判定定理即可得到结论.
解答 证明:连结OD,如图,
∵BD平分∠CBA,
∴∠1=∠2,
∵OB=OD,
∴∠1=∠3,
∴∠2=∠3,
∴OD∥BH,
而BH⊥EF,
∴OD⊥EF,
∴FE是⊙O的切线.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
3.将二次函数y=-2(x+1)2-5的图象向右移动一个单位,再向上移动5个单位后得到的二次函数解析式为( )
| A. | y=-2x2 | B. | y=-2(x-2)2 | C. | y=-2(x-2)2-10 | D. | y=-2x2-10 |
20.下列判断正确的是( )
| A. | 比正数小的数一定是负数 | |
| B. | 有最大的负整数和最小的正整数 | |
| C. | 零是最小的有理数 | |
| D. | 一个有理数所对应的点离开原点越远,则它越大 |
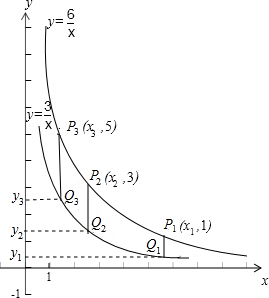 两个反比例函数y=$\frac{3}{x}$,y=$\frac{6}{x}$在第一象限内的图象如图所示,点P1,P2,P3,…,P2015在反比例函数y=$\frac{6}{x}$图象上,它们的横坐标分别是x1,x2,x3,…,x2015,纵坐标分别是1,3,5,…,共2015个连续奇数,过点P1,P2,P3,…,P2015分别作y轴的平行线,与y=$\frac{3}{x}$的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…Q2015(x2015,y2015),则y2015=2014.5.
两个反比例函数y=$\frac{3}{x}$,y=$\frac{6}{x}$在第一象限内的图象如图所示,点P1,P2,P3,…,P2015在反比例函数y=$\frac{6}{x}$图象上,它们的横坐标分别是x1,x2,x3,…,x2015,纵坐标分别是1,3,5,…,共2015个连续奇数,过点P1,P2,P3,…,P2015分别作y轴的平行线,与y=$\frac{3}{x}$的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…Q2015(x2015,y2015),则y2015=2014.5. 已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC. 如图,BD平分∠ABC,∠DBE=29°,且∠CBE比∠ABE的3倍还大18°,求∠CBD的度数.
如图,BD平分∠ABC,∠DBE=29°,且∠CBE比∠ABE的3倍还大18°,求∠CBD的度数.