题目内容
12.(1)如图1,AC=AE,∠1=∠2,∠C=∠E.求证:BC=DE.(2)如图2,在△ABC中,AB=AC,D为BC中点,∠BAD=30°,求∠C的度数.

分析 (1)利用“ASA”证明△ABC≌△ADE,从而得到BC=DE;
(2)利用等腰三角形的性质可判断AD平分∠BAC,则∠BAD=∠CAD=30°,于是可判定△ABC为等边三角形,然后根据等边三角形的性质可得到∠C=60°.
解答 (1)证明:∵∠1=∠2,
∴∠BAC=∠DAE,
在△ABC和△ADE中
$\left\{\begin{array}{l}{∠BAC=∠DAE}\\{AC=AE}\\{∠C=∠E}\end{array}\right.$,
∴△ABC≌△ADE,
∴BC=DE;
(2)解:∵D为BC中点,
∴BD=CD,
∵AB=AC,
∴AD平分∠BAC,
∴∠BAD=∠CAD=30°,
∴∠BAC=60°,
∴△ABC为等边三角形,
∴∠C=60°.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
1.某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下.(单位:千米)
(1)求收工时距A地多远?方位如何?
(2)若每千米耗油0.3升,问共耗油多少升?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -4 | +7 | -9 | +8 | +6 | -5 | -2 |
(2)若每千米耗油0.3升,问共耗油多少升?
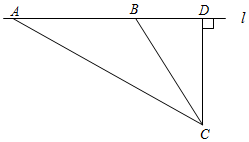 某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于24米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.
某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于24米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.