题目内容
3.在Rt△ABC中,∠C=90°,若cosB=$\frac{4}{5}$,则tanA的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
分析 根据一个角的正弦等于它余角的余弦,可得sin A,根据同角三角函数关系,可得答案.
解答 解:由题意,得
sinA=cosB=$\frac{4}{5}$,
cosA=$\sqrt{1-si{n}^{2}A}$=$\frac{3}{5}$,
tanA=$\frac{sinA}{cosA}$=$\frac{4}{3}$,
故选:D.
点评 本题考查了互余两角三角函数关系,利用一个角的正弦等于它余角的余弦及同角三角函数关系是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11. 如图,△ABC≌△ADE,若∠B=80°,∠C=35°,∠EAC=40°,则∠DAC=( )
如图,△ABC≌△ADE,若∠B=80°,∠C=35°,∠EAC=40°,则∠DAC=( )
 如图,△ABC≌△ADE,若∠B=80°,∠C=35°,∠EAC=40°,则∠DAC=( )
如图,△ABC≌△ADE,若∠B=80°,∠C=35°,∠EAC=40°,则∠DAC=( )| A. | 40° | B. | 35° | C. | 30° | D. | 25° |
18.如果A和B都是三次多项式,则A+B一定是( )
| A. | 三次多项式 | B. | 六次多项式 | ||
| C. | 次数不低于3的整式 | D. | 次数不高于3的整式 |
8.已知△ABC≌△DEF,若△ABC的周长为20,AB=5,BC=6,则DF的长度为( )
| A. | 5 | B. | 6 | C. | 9 | D. | 11 |
15.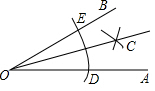 在数学课上,老师用直尺和圆规作角平分线,方法如下:
在数学课上,老师用直尺和圆规作角平分线,方法如下:
作法:①在OA和OB上分别截取OD、OE,使OD=OE.
②分别以D、E为圆心,以大于$\frac{1}{2}$DE的长为半径作弧,两弧在∠AOB内交于点C
③作射线OC,则OC就是∠AOB的平分线
说说老师用尺规作角平分线时,用到的三角形全等的判定方法是( )
 在数学课上,老师用直尺和圆规作角平分线,方法如下:
在数学课上,老师用直尺和圆规作角平分线,方法如下:作法:①在OA和OB上分别截取OD、OE,使OD=OE.
②分别以D、E为圆心,以大于$\frac{1}{2}$DE的长为半径作弧,两弧在∠AOB内交于点C
③作射线OC,则OC就是∠AOB的平分线
说说老师用尺规作角平分线时,用到的三角形全等的判定方法是( )
| A. | SAS | B. | ASA | C. | SSS | D. | AAS |
12.平面直角坐标系内与点P(-2,3)关于原点对称的点的坐标是( )
| A. | (3,-2) | B. | (2,3) | C. | (2,-3) | D. | (-3,-3) |
 如图,已知y1=2x+10与y2=5x+4图象交点的纵坐标是14,则当x≥2时,y1≤y2.
如图,已知y1=2x+10与y2=5x+4图象交点的纵坐标是14,则当x≥2时,y1≤y2.