题目内容
14．抛物线y=2x2-8x+m与两坐标轴共有两个公共点，则m的值为小于8．分析 由抛物线y=2x2-8x+m与x轴有两个公共点可知，对应的一元二次方程2x2-8x+m=0，根的判别式△=b2-4ac＞0，由此即可得到关于m的方程，解方程即可求得m的值．
解答 解：∵抛物线与x轴有两个公共点，
∴△＞0，
∴b2-4ac=82-4×2×m＞0；
∴m＜8．
故答案为：小于8．
点评 本题考查的是抛物线与x轴的交点及根的判别式，熟知抛物线与x轴的交点问题与一元二次方程根的关系是解答此题的关键．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
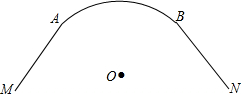由圆弧形弯道$\widehat{AB}$和两段直道AM、BN组成的一条公路示意图如图所示，直线AM、BN分别与$\widehat{AB}$所在的⊙O相切于点A、B．已知⊙O的半径为90m，$\widehat{AB}$的长为60πm，求直线AM与BN所成的锐角的度数，以及AM，BN的交点到⊙O的切线长．
如图，C是以AB为直径的⊙O上一点，已知AC=8，BC=6，则圆O的半径等于5．
6．从长度分别为3，5，6，9的四条线段中任取三条，能组成三角形的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{3}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
3．在Rt△ABC中，∠C=90°，若cosB=$\frac{4}{5}$，则tanA的值是（ ）
| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
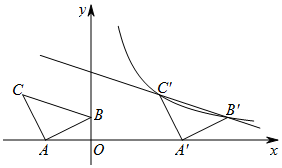如图，在平面直角坐标系中有Rt△ABC，已知∠CAB=90°，AB=AC，A（-2，0），B（0，1）．