题目内容
9. 如图,矩形ABCD中,∠EFC=90°,CF平分∠DCE,S△CDF:S△FAE=16:9,CD=8,则S矩形ABCD=96.
如图,矩形ABCD中,∠EFC=90°,CF平分∠DCE,S△CDF:S△FAE=16:9,CD=8,则S矩形ABCD=96.
分析 首先由矩形ABCD中,∠EFC=90°,CF平分∠DCE,可证得△AEF∽△DFC,△CDF∽△CFE,然后由相似三角形的对应边成比例,求得AF与DF的长,继而求得答案.
解答 解:∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠AEF+∠AFE=90°,
∵∠EFC=90°,
∴∠AFE+∠CFD=90°,
∴∠AEF=∠CFD,
∴△AEF∽△DFC,
∵S△CDF:S△FAE=16:9,
∴CD:AF=FC:EF=4:3,
∵CD=8,
∴AF=6,
∵CF平分∠DCE,
∴∠DCF=∠FCE,
∵∠EFC=∠D=90°,
∴△CDF∽△CFE,
∴CD:DF=FC:EF=4:3,
∴DF=6,
∴AD=AF:DF=12,
∴S矩形ABCD=AD•CD=96.
故答案为:96.
点评 此题考查了相似三角形的判定与性质以及矩形的性质.注意证得△AEF∽△DFC,△CDF∽△CFE是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.下列各式中,不是同类项的是( )
| A. | $\frac{1}{2}$ab和5ba | B. | a3和53 | C. | $\frac{xy}{5}$和52xy | D. | 102和$\frac{1}{10}$ |
4.下列二次根式中与$\sqrt{2}$能合并的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{20}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{18}$ |
14.已知直角三角形的两条直角边分别是3和4,则它斜边上的中线长为( )
| A. | 2.4 | B. | 2.5 | C. | 3 | D. | 5 |
1.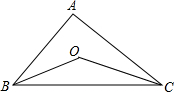 如图,点O是△ABC内一点,∠A=90°,∠ABC与∠ACB的角平分线BO,CO相交点O,则∠BOC等于( )
如图,点O是△ABC内一点,∠A=90°,∠ABC与∠ACB的角平分线BO,CO相交点O,则∠BOC等于( )
 如图,点O是△ABC内一点,∠A=90°,∠ABC与∠ACB的角平分线BO,CO相交点O,则∠BOC等于( )
如图,点O是△ABC内一点,∠A=90°,∠ABC与∠ACB的角平分线BO,CO相交点O,则∠BOC等于( )| A. | 95° | B. | 120° | C. | 135° | D. | 无法确定 |

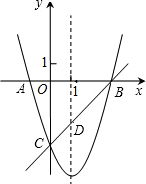 如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.