题目内容
20.△ABO的顶点坐标分别是A(-3,3),B(3,3),O(0,0),若△BOE∽△ABO,则点E的坐标(3,0)或(0,3).分析 先判断△ABO为等腰直角三角形,则利用△BOE∽△ABO得到△BOE为等腰直角三角形,且∠BEO=∠AOB=90°,所以OE=BE=$\frac{\sqrt{2}}{2}$OB=3,然后写出E点坐标.
解答 解:如图,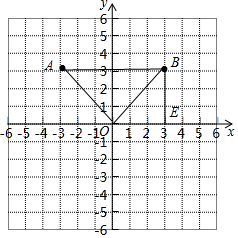 ∵A(-3,3),B(3,3),O(0,0),
∵A(-3,3),B(3,3),O(0,0),
∴AB=6,OA=OB=3$\sqrt{2}$,△ABO为等腰直角三角形,
∵△BOE∽△ABO,
∴△BOE为等腰直角三角形,且∠BEO=∠AOB=90°,
∴OE=BE=$\frac{\sqrt{2}}{2}$OB=3,
∴E点坐标为(3,0)或(0,3).
故答案为(3,0)或(0,3).
点评 本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等.也考查了坐标与图形性质.

练习册系列答案
相关题目
15.下列说法错误的是( )
| A. | -9没有平方根 | B. | ±1是1的平方根 | ||
| C. | -$\frac{1}{64}$的立方根为-$\frac{1}{4}$ | D. | 2的平方根为$\sqrt{2}$ |
 如图,某同学把一块三角形的玻璃打破成了三块,现要到玻璃店去配一块大小、形状完全相同的玻璃,那么他可以带那一块③.
如图,某同学把一块三角形的玻璃打破成了三块,现要到玻璃店去配一块大小、形状完全相同的玻璃,那么他可以带那一块③.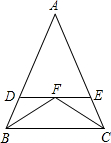 如图,△ABC中AB=AC,BF、CF分别平分∠ABC、∠ACB,过点F作直线DE∥BC,交AB、AC于D、E,则图中共有等腰三角形( )个.
如图,△ABC中AB=AC,BF、CF分别平分∠ABC、∠ACB,过点F作直线DE∥BC,交AB、AC于D、E,则图中共有等腰三角形( )个. 如图,矩形ABCD中,∠EFC=90°,CF平分∠DCE,S△CDF:S△FAE=16:9,CD=8,则S矩形ABCD=96.
如图,矩形ABCD中,∠EFC=90°,CF平分∠DCE,S△CDF:S△FAE=16:9,CD=8,则S矩形ABCD=96. 如图,在∠MON的两边上取A,B两点,连AB,分别以OA,AB为边,在∠MON内作等边△OAD和等边△ABC,连CD,求证:OB=DC.
如图,在∠MON的两边上取A,B两点,连AB,分别以OA,AB为边,在∠MON内作等边△OAD和等边△ABC,连CD,求证:OB=DC.