题目内容
18.已知$\sqrt{a}$、$\sqrt{b}$、$\sqrt{a+b}$均为正整数,请适当选取a、b的值,并求$\sqrt{a}$、$\sqrt{b}$、$\sqrt{a+b}$所组成三角形的面积.分析 由勾股定理逆定理可知以$\sqrt{a}$、$\sqrt{b}$、$\sqrt{a+b}$组成的三角形是直角三角形,再根据$\sqrt{a}$、$\sqrt{b}$、$\sqrt{a+b}$均为正整数,可取可取a=9,b=16,最后由三角形面积公式计算可得.
解答 解:∵($\sqrt{a}$)2+($\sqrt{b}$)2=($\sqrt{a+b}$)2
∴以$\sqrt{a}$、$\sqrt{b}$、$\sqrt{a+b}$组成的三角形是直角三角形,
又∵$\sqrt{a}$、$\sqrt{b}$、$\sqrt{a+b}$均为正整数,
∴可取a=9,b=16,则$\sqrt{a+b}$=5,
∴所组成三角形的面积为:$\frac{1}{2}$×3×4=6.
点评 本题主要考查二次根式的应用及勾股定理逆定理,熟练掌握勾股定理逆定理并据此判断出该三角形为直角三角形是关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
13. 如图,点F是正方形ABCD边CD上的一个动点,BF的垂直平分线EM与对角线AC相交于点E,与BF相交于点M,连接BE、FE,EM=3,则△EBF的周长是( )
如图,点F是正方形ABCD边CD上的一个动点,BF的垂直平分线EM与对角线AC相交于点E,与BF相交于点M,连接BE、FE,EM=3,则△EBF的周长是( )
 如图,点F是正方形ABCD边CD上的一个动点,BF的垂直平分线EM与对角线AC相交于点E,与BF相交于点M,连接BE、FE,EM=3,则△EBF的周长是( )
如图,点F是正方形ABCD边CD上的一个动点,BF的垂直平分线EM与对角线AC相交于点E,与BF相交于点M,连接BE、FE,EM=3,则△EBF的周长是( )| A. | 6+3$\sqrt{2}$ | B. | 6+6$\sqrt{2}$ | C. | 6-3$\sqrt{2}$ | D. | 3+3$\sqrt{2}$ |
10.如果一个三角形的三个外角的度数之比是2:3:4,那么与之对应的三个内角的度数之比是( )
| A. | 1:3:5 | B. | 2:3:4 | C. | 4:3:2 | D. | 5:3:1 |
7.在三角形的三个外角中,锐角最多只有( )个.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
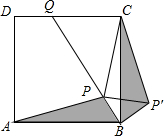 如图,点P是正方形ABCD内一点,点P到点A,B和C的距离分别为$\sqrt{10}$,1,2$\sqrt{2}$,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为45(度)
如图,点P是正方形ABCD内一点,点P到点A,B和C的距离分别为$\sqrt{10}$,1,2$\sqrt{2}$,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为45(度)