题目内容
1.计算题:(1)解不等式3(x-1)<5x+2,并在数轴上表示解集;
(2)解不等式组$\left\{\begin{array}{l}x+4≤6\\ \frac{1}{2}(x-3)>-2\end{array}\right.$,并在数轴上表示解集;
(3)解方程:$\frac{x}{x-1}-\frac{3}{x+1}=1$;
(4)解方程:3x2-6x-2=0.
分析 (1)去括号、移项、合并同类项、系数化成1即可求解;
(2)先求出不等式组中每一个不等式的解集,再求出它们的公共部分,然后把不等式的解集表示在数轴上即可;
(3)去分母化成整式方程,解整式方程求得x的值,然后进行检验即可;
(4)利用分解因式法即可求解.
解答 解:(1)去括号,得3x-3<5x+2,
移项,得3x-5x<2+3,
合并同类项,得-2x<5,
系数化为1得x>-$\frac{5}{2}$, ;
;
(2)$\left\{\begin{array}{l}{x+4≤6…①}\\{\frac{1}{2}(x-3)>-2…②}\end{array}\right.$,
解①得:x≤2,
解②得:x>-1. ,
,
则不等式组的解集是-1<x≤2;
(3)去分母,得x(x+1)-3(x-1)=(x+1)(x-1),
即x2+x-3x+3=x2-1,
移项、合并同类项,得-2x=-4,
系数化为1得x=2.
当x=2时,(x+1)(x-1)≠0,
则x=2是方程的解;
(4)3x2-6x-2=0.
x=$\frac{6±2\sqrt{15}}{6}$,
∴x1=3+$\frac{\sqrt{15}}{3}$,x2=3-$\frac{\sqrt{15}}{3}$.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.要注意x是否取得到,若取得到则x在该点是实心的.反之x在该点是空心的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.2015年我国国民生产总值约28.6万亿元人民币,用科学记数法表示2015年我国国民生产总值为( )
| A. | 28.6×1012元 | B. | 2.86×1012元 | C. | 2.86×1014元 | D. | 2.86×1013元 |
6.4的平方根是( )
| A. | 2 | B. | ±2 | C. | -2 | D. | 不存在 |
 如图,已知AB∥CD,EF⊥AB于点G,若∠1=30°,试求∠F的度数.
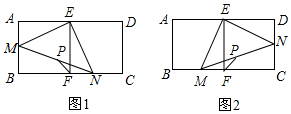
如图,已知AB∥CD,EF⊥AB于点G,若∠1=30°,试求∠F的度数.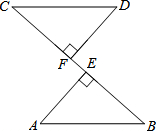 如图,DF=AE,AE⊥BC,DF⊥BC,CE=BF.求证:AB=CD.
如图,DF=AE,AE⊥BC,DF⊥BC,CE=BF.求证:AB=CD.