题目内容
18.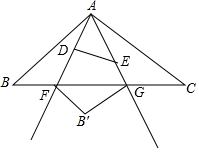 如图,在△ABC中,AB=AC=4,∠BAC=90°,以A为一个顶点的等腰Rt△ADE,∠ADE=90°,绕点A在∠BAC内旋转,AD、AE所在的直线与BC边分别交于点F、G,若点B关于直线AD的对称点为B′,当∠CFB′=60°时,则BF的长为$\frac{6\sqrt{2}-2\sqrt{3}}{3}$.
如图,在△ABC中,AB=AC=4,∠BAC=90°,以A为一个顶点的等腰Rt△ADE,∠ADE=90°,绕点A在∠BAC内旋转,AD、AE所在的直线与BC边分别交于点F、G,若点B关于直线AD的对称点为B′,当∠CFB′=60°时,则BF的长为$\frac{6\sqrt{2}-2\sqrt{3}}{3}$.
分析 把△ACG绕点A顺时针旋转90°得到△ABG′,连结FG′、AB′,如图,则根据旋转的性质得BG′=CG,AG=AG,∠ABG′=∠C=45°,∠1=∠BAG′,所以∠FBG′=90°,再证明△AFG≌△AFG′得到FG=FG′,接着利用对称性质得FB=FB′,AB=AB′,∠2=∠3,易得∠1=∠4,AC=AB′,则可判断△AB′G与△ACG关于AG对称,得到GB′=GC,则GB′=BG′,解直角三角形得到关于BF的方程,然后解关于BF的方程即可.
解答 解:把△ACG绕点A顺时针旋转90°得到△ABG′,连结FG′、AB′,如图,则BG′=CG,AG=AG,∠ABG′=∠C=45°,∠1=∠BAG′,
∴∠FBG′=90°,
∵∠FAG=45°,
∴∠1+∠2=45°,
∴∠FAG′=45°,
在△AFG和△AFG′中,$\left\{\begin{array}{l}{AG=AG′}\\{∠FAG=∠FAG′}\\{AF=AF}\end{array}\right.$,
∴△AFG≌△AFG′,
∴FG=FG′,
∵点B关于直线AD的对称点为B′,
∴FB=FB′,AB=AB′,∠2=∠3,
而∠3+∠4=45°,∠1+∠2=45°,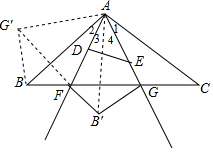
∴∠1=∠4,
而AC=AB=AB′,
∴△AB′G与△ACG关于AG对称,
∴GB′=GC,
∴GB′=BG′,
在△FB′G和△FBG′中,$\left\{\begin{array}{l}{FB′=FB}\\{FG=FG′}\\{B′G=BG′}\end{array}\right.$,
∴△FB′G≌△FBG′,
∴∠GFB′=∠BFG′=60°,∠FB′G=∠FBG′=90°,
在Rt△BFG′中,∵∠FBG′=60°,
∴BG′=$\sqrt{3}$BF,FG′=2BF,
∴CG=$\sqrt{3}$BF,FG=2BF,
∴BF+$\sqrt{3}$BF+2BF=BC=4 $\sqrt{2}$,
∴BF=$\frac{6\sqrt{2}-2\sqrt{3}}{3}$,
故答案为:$\frac{6\sqrt{2}-2\sqrt{3}}{3}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质和对称的性质.

| A. | π的值等于3.14 | B. | π的值是圆周长与直径的比值 | ||
| C. | π的值与圆的大小无关 | D. | π是一个无限小数 |
| A. | 审核书稿中的错别字 | B. | 调查《极限挑战》栏目的收视率 | ||
| C. | 对八名同学的身高情况进行调查 | D. | 对某社区的卫生死角进行调查 |
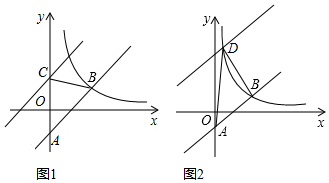
 已知,正六边形ABCDEF在直角坐标系内的位置如图所示,点A的坐标为A(-1,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点B的经过的路径长是(2016$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
已知,正六边形ABCDEF在直角坐标系内的位置如图所示,点A的坐标为A(-1,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点B的经过的路径长是(2016$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).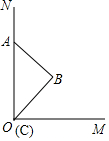 已知OM⊥ON,斜边长为4的等腰直角△ABC的斜边AC在射线上,顶点C与O重合,若点A沿NO方向向O运动,△ABC的顶点C随之沿OM方向运动,点A移动到点O为止,则直角顶点B运动的路径长是8-4$\sqrt{2}$.
已知OM⊥ON,斜边长为4的等腰直角△ABC的斜边AC在射线上,顶点C与O重合,若点A沿NO方向向O运动,△ABC的顶点C随之沿OM方向运动,点A移动到点O为止,则直角顶点B运动的路径长是8-4$\sqrt{2}$.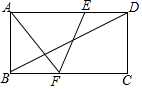 如图,在矩形ABCD中,点E、F分别是AD、BC上的点,连接AF、EF,EF与对角线BD交于点O.若AE=AF=CF=12,∠AEF=2∠ADB,则矩形ABCD的面积为108$\sqrt{3}$.
如图,在矩形ABCD中,点E、F分别是AD、BC上的点,连接AF、EF,EF与对角线BD交于点O.若AE=AF=CF=12,∠AEF=2∠ADB,则矩形ABCD的面积为108$\sqrt{3}$.