题目内容
19. 如图,正方形ABCD的面积为1.△BPC为等边三角形.则△PBD的面积为$\frac{\sqrt{3}-1}{4}$.
如图,正方形ABCD的面积为1.△BPC为等边三角形.则△PBD的面积为$\frac{\sqrt{3}-1}{4}$.
分析 根据△PBD的面积=△PBC的面积+△PCD的面积-△BCD的面积,分别求得各三角形的面积即可得到△PBD的面积.
解答 解:∵正方形ABCD的面积为1,
∴边长是1,
过P作PE⊥CD于E点,则PE=$\frac{1}{2}$AD=$\frac{1}{2}$,
∴△PCD的面积为 $\frac{1}{2}$×CD×PE=$\frac{1}{4}$,△PBC的面积是 $\frac{\sqrt{3}}{4}$,△BCD的面积是 $\frac{1}{2}$,
∴△PBD的面积=△PBC的面积+△PCD的面积-△BCD的面积=$\frac{\sqrt{3}}{4}$+$\frac{1}{4}$-$\frac{1}{2}$=$\frac{\sqrt{3}-1}{4}$.
故答案为$\frac{\sqrt{3}-1}{4}$
点评 本题考查正方形的性质、等边三角形的性质等知识,解题的关键是学会求一个不规则的图形的面积时,可以转化为几个规则图形或易求面积的图形的和或差.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
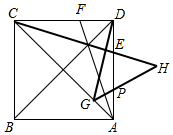 在正方形ABCD中,DE=DF,DG⊥CE,交CA于G,GH⊥AF,交AD于P,交CE延长线于H,请问三条粗线DG,GH,CH的数量关系.
在正方形ABCD中,DE=DF,DG⊥CE,交CA于G,GH⊥AF,交AD于P,交CE延长线于H,请问三条粗线DG,GH,CH的数量关系.
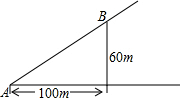 如图,有一个山坡,如果沿山坡在水平AC方向上每前进100m铅直高度就升高60m,那么用科学计算器求坡角∠A的度数,并以“度、分、秒”为单位表示出这个度数,下列按键顺序正确的是( )
如图,有一个山坡,如果沿山坡在水平AC方向上每前进100m铅直高度就升高60m,那么用科学计算器求坡角∠A的度数,并以“度、分、秒”为单位表示出这个度数,下列按键顺序正确的是( )


