题目内容
3.为确保信息安金,信息需加密传输,发送方由明文→密文(加密),接受方由密文→明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d.例如,明文1,2,3,4对应密文5,7,18,16.当明文为2,2,3,3时,求对应的密文.分析 根据“明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d”进行解答.
解答 解:∵明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d,
∴当明文为2,2,3,3时,对应的密文为:2+2×2=6,2×2+3=7,2×3+3×3=15,4×3=12,
∴对应的密文是:6,7,15,12.
点评 本题考查了规律型:数字的变化类.关键是正确理解题意,根据密文与明文之间的关系解题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
13.给出下列计算,其中正确的是( )
| A. | a5+a5=a10 | B. | (2a2)3=6a6 | C. | a8÷a2=a4 | D. | (a3)4=a12 |
14.出租车司机小王驾车在东西方向的街道上行驶,如果把最初的出发点记作0,向东行驶记作正,向西行驶记作负,某天上午行驶的路程如下表(单位:km):
(1)到中午,小王是否回到了最初的出发点?
(2)小王距离最初的出发点最远是多少千米?
(3)小王在上述过程中一共行驶了多少路程?
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 路程 | +5 | -3 | +10 | -8 | -6 | +12 | -10 |
(2)小王距离最初的出发点最远是多少千米?
(3)小王在上述过程中一共行驶了多少路程?
8.已知下列结论:
①将直角三角形的三边同时扩大2倍,得到的一个钝角三角形;
②在平面直角坐标系中点A(2,3)与点B(3,2)表示不同的点;
③实数与数轴上的点一一对应;
④有理数有无限个,无理数有有限个.
其中正确的结论是( )
①将直角三角形的三边同时扩大2倍,得到的一个钝角三角形;
②在平面直角坐标系中点A(2,3)与点B(3,2)表示不同的点;
③实数与数轴上的点一一对应;
④有理数有无限个,无理数有有限个.
其中正确的结论是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ②③④ |
12. 如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
 如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 如图,在△ABC中,AB=AC,点P是边BC上任意一点,求证:AB2-AP2=BP•CP.
如图,在△ABC中,AB=AC,点P是边BC上任意一点,求证:AB2-AP2=BP•CP.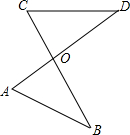 如图所示,AD与BC相交于点O,且$\frac{OA}{OC}$=$\frac{OB}{OD}$,若OA=1.5,OC=2,AB=3,则CD的长为4.
如图所示,AD与BC相交于点O,且$\frac{OA}{OC}$=$\frac{OB}{OD}$,若OA=1.5,OC=2,AB=3,则CD的长为4.