Question

5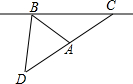．如图，一艘海上巡逻船在A地巡航，测得A地在观测站B的南偏东45°方向上，在观测站C的南偏西60°方向上，观测站B在观测站C的正西方向，此时A地与观测站B的距离为20$\sqrt{2}$海里．
（1）求A地与观测站C的距离是多少海里？
（2）现收到故障船D的求救信号，要求巡逻船从A地马上前去救援（C，A，D共线）．已知D船位于观测站B的南偏西15°方向上，巡逻船的速度是12海里/小时，求巡逻船从A地到达故障船D处需要多少时间？（结果保留小数点后一位，参考数据$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73，$\sqrt{5}$≈2.24）

Answer 1

分析 （1）过点A作AE⊥BC于点E，过点B作BF⊥BC于点B，过点B作BF⊥BC于点B，过点C作CG⊥BC于点C，在Rt△ABE中，利用边角关系求得答案即可；
（2）过点A作AH⊥BD于点H，在Rt△ABH和Rt△ABH中，利用边角关系求得答案即可．

解答 解：如图，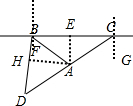

（1）过点A作AE⊥BC于点E，过点B作BF⊥BC于点B，过点B作BF⊥BC于点B，过点C作CG⊥BC于点C，
∵∠ABF=45°，∠ACG=60°，
∴∠ABC=45°，∠ACB=30°，
在Rt△ABE中，AE=AB•sin45°=20$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=20，
∴AC=2AE=40（海里）．
答：A地与观测站C的距离是40海里．
（2）过点A作AH⊥BD于点H，
由题意可知：∠DBF=15°，
∠DBA=60°，∠DBC=105°，
在Rt△ABH中，
AH=AB•sin60°=20$\sqrt{2}$×$\frac{\sqrt{3}}{2}$=10$\sqrt{6}$．
在Rt△ADH中，
AD=$\frac{AH}{sin45°}$=10$\sqrt{6}$×$\sqrt{2}$=20$\sqrt{3}$，
$\frac{AD}{12}$=$\frac{20\sqrt{3}}{12}$≈2.9．
答：巡逻船从A地到达故障船D处需要2.9小时．

点评 此题考查解直角三角形的应用，构造直角三角函数建立边角关系是解决问题的关键．