题目内容
17.从2开始,连续的偶数相加,它们的和的情况如下表:
(1)按这个规律,当m=6时,和为42;
(2)从2开始,m个连续偶数相加,它们的和S与m之间的关系,用公式表示出来为:s=m(m+1).
(3)应用上述公式计算:
①2+4+6+…+200
②202+204+206+…+300.
分析 (1)(2)由计算的算式可以看出:从2开始连续偶数的和,等于加数的个数乘加数的个数加1,由此规律解答即可;
(3)①利用发现的规律直接计算即可;
②把算式变为2+4+6+…+300-(2+4+6+…+200)计算得出答案即可.
解答 解:(1)当m=6时,和为6×7=42;
(2)s=m(m+1);
(3)①2+4+6+…+200
=100×101
=10100;
②202+204+206+…+300
=2+4+6+…+300-(2+4+6+…+200)
=150×151-101×100
=22650-10100
=12550.
点评 此题考查数字的变化规律,找出数字的特点,得出运算的规律:从2开始连续偶数的和,等于加数的个数乘加数的个数加1是解决问题的依据.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列汽车标志不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2.如果|a+2|+|b-1|=0,则a+b的值是( )
| A. | 0 | B. | 1 | C. | -1 | D. | 0或1或-1 |
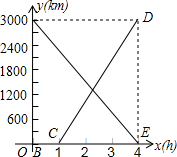 A、B两机场相距3000km,甲、乙两架飞机沿同一航线分别从A、B两机场出发相向而行,假设它们都保持匀速行驶,如图,线段AE、CD分别表示甲、乙两机离B机场的距离y(km)和所用去的时间x(h)之间的函数关系的图象,观察图象回答下列问题:
A、B两机场相距3000km,甲、乙两架飞机沿同一航线分别从A、B两机场出发相向而行,假设它们都保持匀速行驶,如图,线段AE、CD分别表示甲、乙两机离B机场的距离y(km)和所用去的时间x(h)之间的函数关系的图象,观察图象回答下列问题: 某商店“三八节”开展有奖促销活动,他们设立了一个可以自由转动的转盘(如图),转盘被分成3个面积相等的扇形,3个扇形区域里分别标有“10元”、“20元”、“30元”的字样.根据规定:顾客在该商店购买总价每满100元就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,小明的妈妈在该商店购物一次,总价是210元.
某商店“三八节”开展有奖促销活动,他们设立了一个可以自由转动的转盘(如图),转盘被分成3个面积相等的扇形,3个扇形区域里分别标有“10元”、“20元”、“30元”的字样.根据规定:顾客在该商店购买总价每满100元就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,小明的妈妈在该商店购物一次,总价是210元.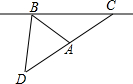 如图,一艘海上巡逻船在A地巡航,测得A地在观测站B的南偏东45°方向上,在观测站C的南偏西60°方向上,观测站B在观测站C的正西方向,此时A地与观测站B的距离为20$\sqrt{2}$海里.
如图,一艘海上巡逻船在A地巡航,测得A地在观测站B的南偏东45°方向上,在观测站C的南偏西60°方向上,观测站B在观测站C的正西方向,此时A地与观测站B的距离为20$\sqrt{2}$海里.