题目内容
2.下列多项式能进行因式分解的是( )| A. | x2-y | B. | x2+1 | C. | x2-6x | D. | x2+y+y2 |
分析 直接利用因式分解的意义结合提取公因式法分解因式的方法进而判断得出即可.
解答 解:A、x2-y无法分解因式,故此选项错误;
B、x2+1无法分解因式,故此选项错误;
C、x2-6x=x(x-6),故此选项正确;
D、x2+y+y2无法分解因式,故此选项错误;
故选:C.
点评 此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.

练习册系列答案
相关题目
13.把分式$\frac{x^2}{x-y}$中的x和y的值都扩大到原来的2倍,则分式的值为( )
| A. | 不变 | B. | 扩大为原来的2倍 | C. | 扩大为原来的4倍 | D. | 缩小为原来的$\frac{1}{2}$ |
10.若点P(a,a-3)在第四象限,则a的取值范围是( )
| A. | a<0 | B. | a>3 | C. | -3<a<0 | D. | 0<a<3 |
17.下列各图中,可以由一个正方形的平面展开图得到的是( )
| A. |  | B. |  | C. |  | D. |  |
7.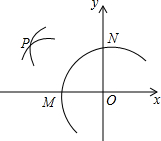 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(m,n-3),则m与n的数量关系为( )
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(m,n-3),则m与n的数量关系为( )
 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(m,n-3),则m与n的数量关系为( )
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(m,n-3),则m与n的数量关系为( )| A. | M-n=-3 | B. | m+n=-3 | C. | m-n=3 | D. | m+n=3 |
12.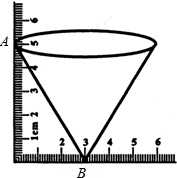 一个圆锥形的漏斗,小李用三角板测得其高度的尺寸如图所示,那么漏斗的斜壁AB的长度为( )
一个圆锥形的漏斗,小李用三角板测得其高度的尺寸如图所示,那么漏斗的斜壁AB的长度为( )
 一个圆锥形的漏斗,小李用三角板测得其高度的尺寸如图所示,那么漏斗的斜壁AB的长度为( )
一个圆锥形的漏斗,小李用三角板测得其高度的尺寸如图所示,那么漏斗的斜壁AB的长度为( )| A. | 4cm | B. | 5cm | C. | 5πcm | D. | $\sqrt{34}$cm |
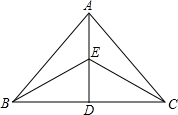 如图△ABC中,D点是BC上的点,E是AD的中点,△BCE的面积是1,则△ABC的面积是( )
如图△ABC中,D点是BC上的点,E是AD的中点,△BCE的面积是1,则△ABC的面积是( )