题目内容
19.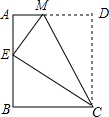 如图,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.
如图,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.(1)求证:△AEM∽△BCE;
(2)若AB=10,BC=8,求四边形ABCM的面积.
分析 (1)如图,首先证明∠A=∠B=90°,证明∠MEC=90°;其次证明∠AME=∠BEC,即可解决问题.
(2)如图,首先求出BE=6,得到AE=4;证明ME=MD(设为λ),运用勾股定理列出关于λ的方程,求出λ;求出△CDM的面积,即可解决问题.
解答  解:(1)如图,∵四边形ABCD为矩形,
解:(1)如图,∵四边形ABCD为矩形,
∴∠A=∠B=∠D=90°;
由题意得:∠CEM=∠D=90°,
∴∠AME+∠AEM=∠AEM+∠BEC,
∴∠AME=∠BEC,
∴△AEM∽△BCE.
(2)∵四边形ABCD为矩形,
∴CD=AB=10;由题意得:
CE=CD=10;由勾股定理得:
BE2=CE2-BC2,而BC=8,
∴BE=6,AE=10-6=4;
由题意得:ME=MD(设为λ),则AM=8
由勾股定理:λ2=42+(8-λ)2,
解得:λ=5,
∴SABCM=SABCD-S△CDM
=10×8-$\frac{1}{2}$×10×5
=80-25=55.
即四边形ABCM的面积=55.
点评 该题主要考查了旋转变换的性质、矩形的性质、勾股定理等几何知识点及其应用问题;解题的方法是深入观察图形,准确找出图形中隐含的相等或相似关系;解题的关键是灵活运用旋转变换的性质等几何知识点来分析、判断、解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.下列各式中,是最简二次根式的是( )
| A. | $\sqrt{a+5}$ | B. | $\sqrt{\frac{a}{3}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{5{a^2}}$ |
10.若点P(a,a-3)在第四象限,则a的取值范围是( )
| A. | a<0 | B. | a>3 | C. | -3<a<0 | D. | 0<a<3 |
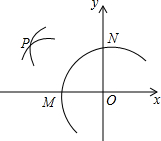 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(m,n-3),则m与n的数量关系为( )
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(m,n-3),则m与n的数量关系为( ) 如图所示,把一块长方形纸片ABCD沿EF折叠,若∠EFB=58°,则∠BFN=64°.
如图所示,把一块长方形纸片ABCD沿EF折叠,若∠EFB=58°,则∠BFN=64°.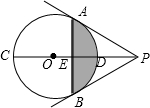 如图,CD为⊙O的直径,P是CD延长线上一点,PA为⊙O的切线,点A为切点,过A点作AB⊥PC,交PC于E,交⊙O于B,连结PB.
如图,CD为⊙O的直径,P是CD延长线上一点,PA为⊙O的切线,点A为切点,过A点作AB⊥PC,交PC于E,交⊙O于B,连结PB.