Question

4．如图，△ABC中，∠ACB=90°，AC=5，BC=12，CO⊥AB于点O，D是线段OB上一点，DE=2，ED∥AC（∠ADE＜90°），连接BE、CD．设BE、CD的中点分别为P、Q．
（1）求AO的长；
（2）求PQ的长；
（3）设PQ与AB的交点为M，请直接写出|PM-MQ|的值．

Answer 1

分析 （1）由△ABC∽△ACO，得$\frac{AB}{AC}$=$\frac{AC}{AO}$，由此即可求出OA．
（2）如图2中，取BD中点F，CD中点Q，连接PF、QF，在Rt△PFQ中，求出PF，QF即可解决问题．
（3）如图3中，取AD中点G，连接GQ，由PF∥GQ，推出△PMF∽△QMG，推出$\frac{PM}{QM}$=$\frac{PF}{QG}$=$\frac{2}{5}$，由PM+QM=$\sqrt{37}$，可以求出PM，QM，即可解决问题．

解答 解：（1）如图1中，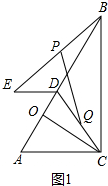

∵CO⊥AB，
∴∠AOC=∠ACB=90°，∵∠A=∠A，
∴△ABC∽△ACO，
∴$\frac{AB}{AC}$=$\frac{AC}{AO}$，
∵AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13，
∴OA=$\frac{A{C}^{2}}{AB}$=$\frac{25}{13}$．

（2）如图2中，取BD中点F，CD中点Q，连接PF、QF，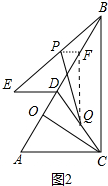

则PF∥ED，FQ∥BC，PF⊥FQ，且PF=$\frac{1}{2}$ED=1，FQ=$\frac{1}{2}$BC=6，
在Rt△PFQ中，PQ=$\sqrt{P{F}^{2}+F{Q}^{2}}$=$\sqrt{{1}^{2}+{6}^{2}}$=$\sqrt{37}$．

（3）如图3中，取AD中点G，连接GQ，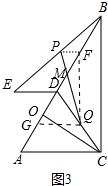

∵GQ∥AC，ED∥AC，PF∥ED，
∴PF∥GQ，
∴△PMF∽△QMG，
∴$\frac{PM}{QM}$=$\frac{PF}{QG}$=$\frac{2}{5}$，
∵PM+QM=$\sqrt{37}$，
∴PM=$\frac{2\sqrt{37}}{7}$，MQ=$\frac{5\sqrt{37}}{7}$，
∴|PM-QM|=$\frac{3\sqrt{37}}{7}$．

点评 本题考查三角形相似综合题、平行线的性质、勾股定理、相似三角形的判定和性质、解题的关键是学会添加常用辅助线，构造特殊三角形以及相似三角形解决问题，属于中考压轴题．