Question

12．课外兴趣小组活动时，老师提出了如下问题：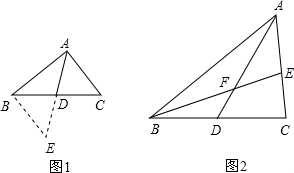

如图1，△ABC中，若AB=8，AC=6，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE=AD，请根据小明的方法思考：
（1）由已知和作图能得到△ADC≌△EDB的理由是B．
A．SSS　　　　　　B．SAS　　　　　　C．AAS　　　　　　　　D．HL
（2）求得AD的取值范围是C．
A．6＜AD＜8　　　B．6≤AD≤8　　C．1＜AD＜7　　D．1≤AD≤7
（3）如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AE=EF．求证：AC=BF．

Answer 1

分析 （1）根据AD=DE，∠ADC=∠BDE，BD=DC推出△ADC和△EDB全等即可；
（2）根据全等得出BE=AC=6，AE=2AD，由三角形三边关系定理得出8-6＜2AD＜8+6，求出即可；
（3）延长AD到M，使AD=DM，连接BM，根据SAS证△ADC≌△MDB，推出BM=AC，∠CAD=∠M，根据AE=EF，推出∠CAD=∠AFE=∠BFD，求出∠BFD=∠M，根据等腰三角形的性质求出即可．

解答 （1）解：∵在△ADC和△EDB中
$\left\{\begin{array}{l}{AD=DE}\\{∠ADC=∠BDE}\\{BD=CD}\end{array}\right.$，
∴△ADC≌△EDB（SAS），
故选B；

（2）解：∵由（1）知：△ADC≌△EDB，
∴BE=AC=6，AE=2AD，
∵在△ABE中，AB=8，由三角形三边关系定理得：8-6＜2AD＜8+6，
∴1＜AD＜7，
故选C．

（3）证明：
延长AD到M，使AD=DM，连接BM，
∵AD是△ABC中线，
∴BD=DC，
∵在△ADC和△MDB中
$\left\{\begin{array}{l}{BD=DC}\\{∠ADC=∠BDM}\\{AD=DM}\end{array}\right.$，
∴△ADC≌△MDB（SAS），
∴BM=AC，∠CAD=∠M，
∵AE=EF，
∴∠CAD=∠AFE，
∵∠AFE=∠BFD，
∴∠BFD=∠CAD=∠M，
∴BF=BM=AC，
即AC=BF．

点评 本题考查了三角形的中线，三角形的三边关系定理，等腰三角形性质和判定，全等三角形的性质和判定等知识点，主要考查学生运用定理进行推理的能力．