题目内容
12.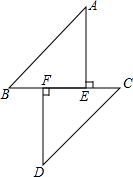 如图,B、E、F、C在同一直线上,AE⊥BC,DF⊥BC,AB=DC,BF=CE,试判断AB与CD的位置关系.
如图,B、E、F、C在同一直线上,AE⊥BC,DF⊥BC,AB=DC,BF=CE,试判断AB与CD的位置关系.
分析 首先由BF=CE,得出BE=CF,利用HL证得△ABE≌△CDF,得出∠B=∠C,判定AB与CD平行即可.
解答 解:AB∥CD.
∵B、E、F、C在同一直线上,BF=CE,
∴BF+EF=CE+EF,
∴BE=CF,
∵AE⊥BC,DF⊥BC,
∴在Rt△ABE和RtCDF中,
$\left\{\begin{array}{l}{AB=CD}\\{BE=CF}\end{array}\right.$,
∴△ABE≌△CDF,
∴∠B=∠C,
∴AB∥CD.
点评 此题考查三角形全等的判定与性质,平行线的判定,掌握三角形全等的判定方法是解决问题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
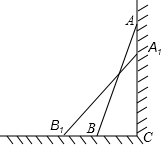 小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真地探索.思考题.如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真地探索.思考题.如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?