题目内容
17.把方程3x(x-1)=(x+2)(x-2)+9化成ax2+bx+c=0的形式为2x2-3x-5=0.分析 方程整理为一般形式即可.
解答 解:方程整理得:3x2-3x=x2-4+9,
即2x2-3x-5=0.
故答案为:2x2-3x-5=0.
点评 此题考查了一元二次方程的一般形式,一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0)特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.

练习册系列答案
相关题目
2.对抛物线y=-x2+2x-3而言,下列结论正确的是( )
| A. | 对称轴x=-1 | B. | 开口向上 | ||
| C. | 与y轴的交点坐标是(0,3) | D. | 函数有最大值,最大值是-2 |
9.x2-3x+4=0的常数项是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.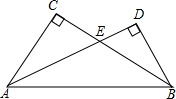 如图,在Rt△ABC与Rt△ABD中,∠C=∠D=90°,AD与BC相交于点E,则∠CAE与∠DBE的大小关系是( )
如图,在Rt△ABC与Rt△ABD中,∠C=∠D=90°,AD与BC相交于点E,则∠CAE与∠DBE的大小关系是( )
 如图,在Rt△ABC与Rt△ABD中,∠C=∠D=90°,AD与BC相交于点E,则∠CAE与∠DBE的大小关系是( )
如图,在Rt△ABC与Rt△ABD中,∠C=∠D=90°,AD与BC相交于点E,则∠CAE与∠DBE的大小关系是( )| A. | ∠CAE>∠DBE | B. | ∠CAE=∠DBE | C. | ∠CAE<∠DBE | D. | 无法确定 |
7.若一个一元二次方程的两根为$\sqrt{2}$+1,$\sqrt{2}$-1,则这个方程是( )
| A. | x2+2$\sqrt{2}$x+1=0 | B. | x2-2$\sqrt{2}$x-1=0 | C. | x2-2$\sqrt{2}$x+1=0 | D. | x2+2$\sqrt{2}$x-1=0 |
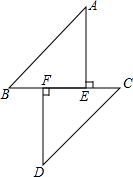 如图,B、E、F、C在同一直线上,AE⊥BC,DF⊥BC,AB=DC,BF=CE,试判断AB与CD的位置关系.
如图,B、E、F、C在同一直线上,AE⊥BC,DF⊥BC,AB=DC,BF=CE,试判断AB与CD的位置关系.