题目内容
20.如果关于x的方程k2x2-(2k+1)x+1=0有实数根,那么k的取值范围是k≥-$\frac{1}{4}$.分析 分类讨论方程是一元一次方程和一元二次方程两种情况讨论,若是一元二次方程直接根据一元二次方程的定义和根的判别式的意义得到k2≠0且△=(2k+1)2-4k2≥0,然后求出两个不等式解的公共部分即可,综合求出k的取值范围.
解答 解:当方程是一元一次方程时,k=0,符合题意,
当方程是一元二次方程时,k≠0,
根据题意得k2≠0且△=(2k+1)2-4k2≥0,
解得k≥-$\frac{1}{4}$且k≠0,
综上可知k≥-$\frac{1}{4}$;
故答案为k≥-$\frac{1}{4}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义,此题涉及到分类讨论的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.x2-3x+4=0的常数项是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
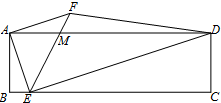 如图,矩形ABCD中,E为BC边上一点,且AE⊥DE.将线段AE绕A点逆时针旋转90°,得到线段AF.连接EF,交AD于点M,连接DF.若BE=1,EF=2$\sqrt{5}$,则点M到DF的距离为$\frac{3}{4}$$\sqrt{2}$.
如图,矩形ABCD中,E为BC边上一点,且AE⊥DE.将线段AE绕A点逆时针旋转90°,得到线段AF.连接EF,交AD于点M,连接DF.若BE=1,EF=2$\sqrt{5}$,则点M到DF的距离为$\frac{3}{4}$$\sqrt{2}$.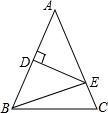 如图,在△ABC中,AC=12cm,ED垂直平分AB,如果△EBC的周长是20cm,那么BC的长度为8cm.
如图,在△ABC中,AC=12cm,ED垂直平分AB,如果△EBC的周长是20cm,那么BC的长度为8cm.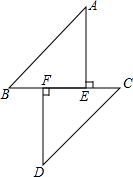 如图,B、E、F、C在同一直线上,AE⊥BC,DF⊥BC,AB=DC,BF=CE,试判断AB与CD的位置关系.
如图,B、E、F、C在同一直线上,AE⊥BC,DF⊥BC,AB=DC,BF=CE,试判断AB与CD的位置关系.