题目内容
20.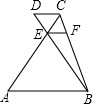 如图,AB∥DC,AC与BD 交于点E,EF∥DC交BC于点F,CE=5,CF=4,AE=BC,则$\frac{DC}{AB}$等于( )
如图,AB∥DC,AC与BD 交于点E,EF∥DC交BC于点F,CE=5,CF=4,AE=BC,则$\frac{DC}{AB}$等于( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{5}$ |
分析 要求$\frac{DC}{AB}$的值,只要先证明△DCE∽△BAE,求出对应边的比即可,根据EF∥DC交BC于点F,CE=5,CF=4,AE=BC,可以得到△CEF∽△CAB,从而求得AE的长,进而可以求得△DCE∽△BAE,和对应边的比,本题得以解决.
解答 解:∵EF∥DC交BC于点F,CE=5,CF=4,AE=BC,
∴△CEF∽△CAB,
∴$\frac{CE}{CA}=\frac{CF}{CB}$,
即$\frac{5}{5+AE}=\frac{4}{BC}$,
∴$\frac{5}{5+AE}=\frac{4}{AE}$,
解得,AE=20,
∵AB∥DC,
∴△DCE∽△BAE,
∴$\frac{DC}{AB}=\frac{CE}{AE}$,
即$\frac{DC}{AB}=\frac{5}{20}=\frac{1}{4}$,
故选B.
点评 本题考查相似三角形的判定与性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用相似三角形的性质解答.

练习册系列答案
相关题目
10.某射击运动员在同一条件下进行射击,结果如表所示:
(1)完成表格;
(2)根据表格,画出该运动员击中靶心的频率的折线统计图;
(3)观察画出的折线统计图,击中靶心的频率的变化有什么规律?
| 射击总次数n | 10 | 20 | 50 | 100 | 200 | 500 | 1000 |
| 击中靶心次数m | 9 | 16 | 41 | 88 | 168 | 429 | 861 |
| 击中靶心频率 $\frac{m}{n}$ | 0.9 | 0.8 | 0.82 | 0.88 | 0.84 | 0.858 | 0.861 |
(2)根据表格,画出该运动员击中靶心的频率的折线统计图;
(3)观察画出的折线统计图,击中靶心的频率的变化有什么规律?
11.合肥市城市轨道交通2号线东起长江东路与大众路交口,西起长江西路与长宁火道交口,线路全长27.8公里,全部为地下线,全线共设车站24座,预计2017年10月1日开始运营,该项目总投资约190亿元.其中190亿用科学记数法表示为( )
| A. | 190×lO8 | B. | 1.9×1010 | C. | 0.19×1011 | D. | 19×109 |
8.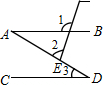 如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠2=80°,那么∠3的度数为( )
如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠2=80°,那么∠3的度数为( )
 如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠2=80°,那么∠3的度数为( )
如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠2=80°,那么∠3的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
15.计算4-(-5)的结果是( )
| A. | 9 | B. | 1 | C. | -1 | D. | -9 |
5.某市在一次空气污染指数抽查中,收集到10天的数据如下:61,75,70,56,81,91,92,91,75,81.该组数据的中位数是( )
| A. | 77.3 | B. | 91 | C. | 81 | D. | 78 |
12.一组数据:a-1,a,a,a+1,若添加一个数据a,下列说法错误的是( )
| A. | 平均数不变 | B. | 中位数不变 | C. | 众数不变 | D. | 方差不变 |
9.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{9}$ | B. | $\sqrt{12}$ | C. | $\sqrt{7}$ | D. | $\sqrt{\frac{1}{3}}$ |
10.一个甲醛分子的大小在0.27纳米左右,1纳米=10-9米,0.27纳米用科学记数法可表示为( )
| A. | 0.27×10-9米 | B. | 2.7×10-10米 | C. | 27×10-7米 | D. | 2.7×108米 |