题目内容
5.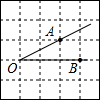 如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB=$\frac{1}{2}$.
如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB=$\frac{1}{2}$.
分析 先在图中找出∠AOB所在的直角三角形,再根据三角函数的定义即可求出tan∠AOB的值.
解答  解:过点A作AD⊥OB垂足为D,
解:过点A作AD⊥OB垂足为D,
如图,在直角△ABD中,AD=1,OD=2,
则tan∠AOB=$\frac{AD}{OD}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了锐角三角函数的概念:在直角三角形中,正弦等于对边比斜边;余弦等于邻边比斜边;正切等于对边比邻边.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
15.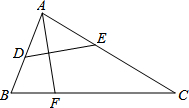 如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折,使点A落在BC边上的点F处,则CE的最大值为( )
如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折,使点A落在BC边上的点F处,则CE的最大值为( )
 如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折,使点A落在BC边上的点F处,则CE的最大值为( )
如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折,使点A落在BC边上的点F处,则CE的最大值为( )| A. | $\frac{8}{3}$ | B. | $\frac{16}{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
13.下面每个表格中的四个数都是按相同规律填写的:
根据此规律确定x的值为( )

根据此规律确定x的值为( )
| A. | 135 | B. | 170 | C. | 209 | D. | 252 |
14.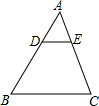 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )| A. | $\frac{AE}{AC}$=$\frac{1}{2}$ | B. | $\frac{DE}{BC}$=$\frac{1}{2}$ | ||
| C. | $\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$ | D. | $\frac{△ADE的面积}{△ABC的面积}$=$\frac{1}{3}$ |
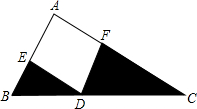 如图,在直角三角形ABC中,∠A=90°,点D在斜边BC上,点E,F分别在直角边AB,AC上,且BD=5,CD=9,四边形AEDF是正方形,则阴影部分的面积为$\frac{45}{2}$.
如图,在直角三角形ABC中,∠A=90°,点D在斜边BC上,点E,F分别在直角边AB,AC上,且BD=5,CD=9,四边形AEDF是正方形,则阴影部分的面积为$\frac{45}{2}$.


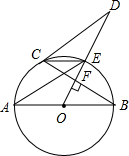 如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE、AE、CD,若∠AEC=∠ODC.
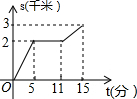
如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE、AE、CD,若∠AEC=∠ODC.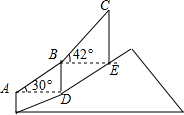 如图,登山缆车从点A出发,途经点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C的垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
如图,登山缆车从点A出发,途经点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C的垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90) 如图,A、B、C三点在⊙O上,且∠AOB=70°,则∠C=35度.
如图,A、B、C三点在⊙O上,且∠AOB=70°,则∠C=35度.