题目内容
4.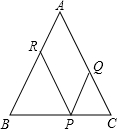 如图,P是等腰△ABC的底边BC上的一点,过P作AB,AC的平行线交AC,AB于点Q,R,证明:PQ+PR为定值.
如图,P是等腰△ABC的底边BC上的一点,过P作AB,AC的平行线交AC,AB于点Q,R,证明:PQ+PR为定值.再考虑以下问题:
(1)若点P在△ABC的内部,可以得到类似的结论吗?若不行,能否对P点再加上某种条件,使类似结论成立?
(2)若点P在BC延长线上,能否发现什么新结论?
(3)若点P是△ABC的BC边上一点,过点P作AB,AC的平行线交AC,AB于点Q,R,试说明若PQ+PR等于AB或AC,则△ABC是等腰三角形.
分析 (1)根据AB∥PQ,AC∥PR,得到四边形ARPQ为平行四边形,所以PQ=AR,PR=AQ,得到PQ+PR=AR+PR=AB=AC.
(2)证明同(1)类似;
(3)根据平行四边形的判定定理,先证明四边形ARPQ为平行四边形,由平行四边形的性质得到PQ=AR=CQ,PR=AQ,得到∠C=∠QPC,又PQ平行于AB,得到∠B=∠C,所以△ABC为等腰三角形.
解答 解:(1)∵AB∥PQ,AC∥PR,
∴四边形ARPQ为平行四边形,
∴PQ=AR,PR=AQ,
∴PQ+PR=AR+PR=AB=AC.
(2)如图: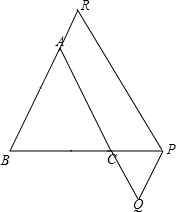
∵AB∥PQ,AC∥PR,
∴四边形ARPQ为平行四边形,
∴PQ=AR,PR=AQ,
∵PQ∥AB,
∴∠B=∠CPQ,
∵∠B=∠ACB,∠ACB=∠PCQ,
∴∠CPQ=∠PCQ,
∴PQ=CQ,
∴PR-PQ=AQ-PQ=AQ-CQ=AC,
即PR-PQ=AB;
(3)∵过点P作AB、AC平行于PQ,PR,PQ+PR=AB(AC),
∴四边形ARPQ为平行四边形,PQ=AR=CQ,PR=AQ,
∴∠C=∠QPC,
又∵PQ平行于AB,
∴∠B=∠C,
∴△ABC为等腰三角形.
点评 本题考查了平行四边形的性质与判定、等腰三角形的性质,解决本题的关键是熟记平行四边形的性质与判定.

练习册系列答案
相关题目
14.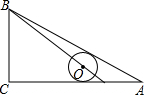 在△ABC中,∠C=90°,∠A=30°,BC=1,点P在AC上,∠PBC=45°,⊙O的圆心在线段BP上,且⊙O与AB,AC都相切,则⊙O的半径是( )
在△ABC中,∠C=90°,∠A=30°,BC=1,点P在AC上,∠PBC=45°,⊙O的圆心在线段BP上,且⊙O与AB,AC都相切,则⊙O的半径是( )
 在△ABC中,∠C=90°,∠A=30°,BC=1,点P在AC上,∠PBC=45°,⊙O的圆心在线段BP上,且⊙O与AB,AC都相切,则⊙O的半径是( )
在△ABC中,∠C=90°,∠A=30°,BC=1,点P在AC上,∠PBC=45°,⊙O的圆心在线段BP上,且⊙O与AB,AC都相切,则⊙O的半径是( )| A. | 2-$\sqrt{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{3}}{6}$ |
14.下列说法中,正确的是( )
| A. | 互为邻补角的两个角一定不相等 | B. | 互为对顶角的两个角有可能不相等 | ||
| C. | 互为内错角的两个角一定相等 | D. | 互为同旁内角的两个角有可能相等 |
 如图,在△ABC中,AG=BG,BD=DE=EC,AC=4AF,若四边形DEFG的面积为11,则△ABC的面积为24.
如图,在△ABC中,AG=BG,BD=DE=EC,AC=4AF,若四边形DEFG的面积为11,则△ABC的面积为24. 如图,△ABC为等边三角形,D为BA延长线上一点,E为线段BC上一点,连接DE、DC,且∠BDE=∠ACD,求证:AD=BE.
如图,△ABC为等边三角形,D为BA延长线上一点,E为线段BC上一点,连接DE、DC,且∠BDE=∠ACD,求证:AD=BE.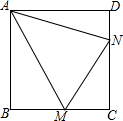 已知正方形ABCD中,∠MAN=45°,且∠MAN的两边分别交BC、DC于点M、N.试猜想线段BM、DN和MN之间的数量关系,写出猜想,并加以证明.
已知正方形ABCD中,∠MAN=45°,且∠MAN的两边分别交BC、DC于点M、N.试猜想线段BM、DN和MN之间的数量关系,写出猜想,并加以证明.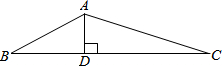 已知:如图,△ABC中,AD⊥BC于点D,AD:BD=2:3,BD:DC=4:5,求tanC的值.
已知:如图,△ABC中,AD⊥BC于点D,AD:BD=2:3,BD:DC=4:5,求tanC的值.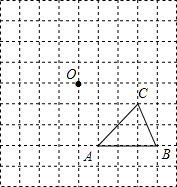 如图,在一个9×9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为1个单位长度.
如图,在一个9×9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为1个单位长度.