题目内容
9.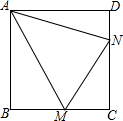 已知正方形ABCD中,∠MAN=45°,且∠MAN的两边分别交BC、DC于点M、N.试猜想线段BM、DN和MN之间的数量关系,写出猜想,并加以证明.
已知正方形ABCD中,∠MAN=45°,且∠MAN的两边分别交BC、DC于点M、N.试猜想线段BM、DN和MN之间的数量关系,写出猜想,并加以证明.
分析 延长CB到E,使BE=DN,连接AE,根据SAS证△ABE≌△ADN,推出AE=AN,∠DAN=∠BAE,求出∠NAM=∠MAE,根据SAS证出△NAM≌△EAM,从而得到BM+DN=MN.
解答 解:BM+DN=MN.
理由:如图,延长CB至E使得BE=DN,连接AE,
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABC=90°=∠ABE,
在△ADN和△ABE中$\left\{\begin{array}{l}{AD=AB}\\{∠D=∠ABE}\\{DN=BE}\end{array}\right.$,
△ABE≌△ADN(SAS),
∴∠BAE=∠DAN,AE=AN,
∴∠EAN=∠BAE+∠BAN=∠DAN+∠BAN=90°,
∵∠MAN=45°,
∴∠EAM=∠MAN,
∵在△EAM和△NAM中,$\left\{\begin{array}{l}{AE=AN}\\{∠EAM=∠NAM}\\{AM=AM}\end{array}\right.$,
∴△EAM≌△NAM,
∴MN=ME,
∵ME=BM+BE=BM+DN,
∴BM+DN=MN.
点评 本题考查了正方形的性质,全等三角形的性质和判定,掌握此类问题辅助线的作法是解题的关键.

练习册系列答案
相关题目
14.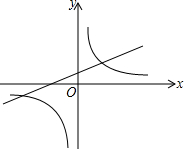 如图,是函数y=kx+1与y=$\frac{k}{x}$(k≠0)在同一直角坐标系中的大致图象,则下列结论正确的是( )
如图,是函数y=kx+1与y=$\frac{k}{x}$(k≠0)在同一直角坐标系中的大致图象,则下列结论正确的是( )
 如图,是函数y=kx+1与y=$\frac{k}{x}$(k≠0)在同一直角坐标系中的大致图象,则下列结论正确的是( )
如图,是函数y=kx+1与y=$\frac{k}{x}$(k≠0)在同一直角坐标系中的大致图象,则下列结论正确的是( )| A. | k<1 | B. | k>0 | C. | k<0 | D. | k>1 |
19.下列各组数中,不是勾股数的是( )
| A. | 13、5、12 | B. | 4、5、6 | C. | 3、4、5 | D. | 15、20、25 |
 如图所示,在平面直角坐标系中,已知A(0,1)、B(2,0)、C(4,3).
如图所示,在平面直角坐标系中,已知A(0,1)、B(2,0)、C(4,3).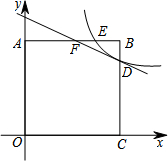 如图,正方形AOCB的边长为4,反比例函数y=$\frac{k}{x}$的图象过点E(3,4),与线段BC交于点D,直线y=-$\frac{1}{2}$x+b过点D,与线段AB相交于点F,连接OF,OE,请你探究∠AOF与∠EOC的数量关系,并证明.
如图,正方形AOCB的边长为4,反比例函数y=$\frac{k}{x}$的图象过点E(3,4),与线段BC交于点D,直线y=-$\frac{1}{2}$x+b过点D,与线段AB相交于点F,连接OF,OE,请你探究∠AOF与∠EOC的数量关系,并证明.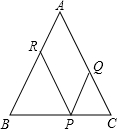 如图,P是等腰△ABC的底边BC上的一点,过P作AB,AC的平行线交AC,AB于点Q,R,证明:PQ+PR为定值.
如图,P是等腰△ABC的底边BC上的一点,过P作AB,AC的平行线交AC,AB于点Q,R,证明:PQ+PR为定值.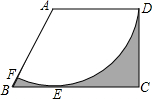 如图,在直角梯形ABCD中,AD∥BC,DC⊥BC,以点A为圆心,AD为半径的圆与BC相切于点E,与AB相交于点F,若AD=$\sqrt{3}$,BE=1,则图中阴影部分的面积为3$+\frac{\sqrt{3}}{2}-π$.
如图,在直角梯形ABCD中,AD∥BC,DC⊥BC,以点A为圆心,AD为半径的圆与BC相切于点E,与AB相交于点F,若AD=$\sqrt{3}$,BE=1,则图中阴影部分的面积为3$+\frac{\sqrt{3}}{2}-π$.