题目内容
13.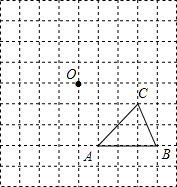 如图,在一个9×9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为1个单位长度.
如图,在一个9×9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为1个单位长度.(1)在网格中画出△ABC向上平移4个单位后得到的△A1B1C1;
(2)在网格中画出△ABC绕点A逆时针旋转90°后得到的△AB2C2,求点C变换到C2的路径长;
(3)在网格中画出△ABC关于点O的中心对称图形△A3B3C3.
分析 (1)根据平移的性质画出点A、B、C平移后的对应点A1、B1、C1即可得到△A1B1C1;
(2)利用网格特点,根据旋转的性质画出点B、C旋转后的对应点B2、C2即可得到△AB2C2,由于点C变换到C2的路径是以点A为圆心、AC为半径,圆心角为90°的弧,所以根据弧长公式可计算出点C变换到C2的路径长;
(3)根据中心对称的性质画出点A、B、C的对应点A3、B3、C3即可得到△A3B3C3.
解答 解:(1)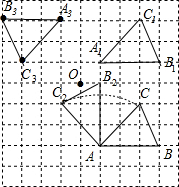 如图,△A1B1C1为所作;
如图,△A1B1C1为所作;
(2)如图,△AB2C2为所作;
AC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
所以点C变换到C2的路径长=$\frac{90•π•2\sqrt{2}}{180}$=$\sqrt{2}$π;
(3)如图,△A3B3C3为所作.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
8.已知二次函数y=2(x-3)2+1.下列说法:
①其图象的开口向下;
②其图象的对称轴为直线x=-3;
③其图象顶点坐标为(3,-1);
④当x<3时,y随x的增大而减小.
其中正确的说法有( )
①其图象的开口向下;
②其图象的对称轴为直线x=-3;
③其图象顶点坐标为(3,-1);
④当x<3时,y随x的增大而减小.
其中正确的说法有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
5.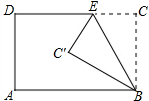 如图所示,将矩形ABCD沿BE折叠,若∠ABC′=30°,则∠BEC′等于( )
如图所示,将矩形ABCD沿BE折叠,若∠ABC′=30°,则∠BEC′等于( )
 如图所示,将矩形ABCD沿BE折叠,若∠ABC′=30°,则∠BEC′等于( )
如图所示,将矩形ABCD沿BE折叠,若∠ABC′=30°,则∠BEC′等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
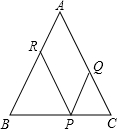 如图,P是等腰△ABC的底边BC上的一点,过P作AB,AC的平行线交AC,AB于点Q,R,证明:PQ+PR为定值.
如图,P是等腰△ABC的底边BC上的一点,过P作AB,AC的平行线交AC,AB于点Q,R,证明:PQ+PR为定值.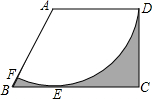 如图,在直角梯形ABCD中,AD∥BC,DC⊥BC,以点A为圆心,AD为半径的圆与BC相切于点E,与AB相交于点F,若AD=$\sqrt{3}$,BE=1,则图中阴影部分的面积为3$+\frac{\sqrt{3}}{2}-π$.
如图,在直角梯形ABCD中,AD∥BC,DC⊥BC,以点A为圆心,AD为半径的圆与BC相切于点E,与AB相交于点F,若AD=$\sqrt{3}$,BE=1,则图中阴影部分的面积为3$+\frac{\sqrt{3}}{2}-π$. 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为2.
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为2.